
Mendive. Journal on Education, January-March 2023; 21(1): e3230 
Translated from the original in Spanish
Original article
Technology, creativity and logical-mathematical thinking: a triad to rethink
Tecnología, creatividad y pensamiento lógico-matemático: una triada para repensar
Tecnologia, criatividade e pensamento lógico-matemático: uma tríade para repensar
Emperatriz Salazar Reyes1![]() https://orcid.org/0000-0002-4200-4128
https://orcid.org/0000-0002-4200-4128
1San Gregorio de Portoviejo University, Manabí, Ecuador. ![]() jempesalar79@hotmail.com
jempesalar79@hotmail.com
| Salazar Reyes, J. (2023). Technology, creativity and logical-mathematical thinking: a triad to rethink. Mendive. Revista de Educación, 21(1), e3230. https://mendive.upr.edu.cu/index.php/MendiveUPR/article/view/3230 |
Received: October 20, 2022.
Accepted: November 30, 2022.
ABSTRACT
According to the latest study by the National Institute for Educational Evaluation, Ecuador is among the countries with the greatest difficulty in the development of skills and abilities, with the lowest level in mathematical knowledge (it did not even reach level 2). That is why the need arises to induce young people to boost their creativity with the use of logic to solve mathematical problems. This article was carried out to present the result of the construction of useful didactic strategies in the educational process of mathematics, identifying the capacities for problem solving in the students of the Educational Unit "Manuel Inocencio Parrales y Guale" of the Jipijapa Canton. It was elaborated from a non-experimental design with quantitative cross-sectional techniques and descriptive and correlational level. In the field work, a battery of questions for students and a survey of teachers in the area of mathematics were applied. The results show that 76.9% of the students have a grade of less than or equal to six points, which means that they have not exceeded the required learning levels in problem solving. The results of the surveys of teachers show that 80% of them apply technological tools and innovative strategies, 20% use technological tools and video games to improve their teachings. It is concluded that laterality in students contributes moderately to serialization, identification and comparison, technology serves as a knowledge management tool that favors learning, facilitates the completion of tasks, favors communication, research and obtaining information.
Keywords: creativity; didactic strategy; mathematical ability; logical-mathematical thinking; Problem resolution.
RESUMEN
Según el último estudio del Instituto Nacional de Evaluación Educativa, Ecuador está entre los países con mayor dificultad en el desarrollo de destrezas y habilidades, con el nivel más bajo en conocimientos matemáticos (ni siquiera alcanzó el nivel 2). Es por eso que surge la necesidad de inducir a los jóvenes a impulsar su creatividad con el uso de la lógica para la resolución de problemas matemáticos. Este artículo se realizó para presentar el resultado de la construcción de estrategias didácticas útiles en el proceso educativo de las matemáticas, identificando las capacidades para la resolución de problemas en los estudiantes de la Unidad Educativa "Manuel Inocencio Parrales y Guale" del Cantón Jipijapa. Se elaboró a partir de un diseño no experimental con técnicas cuantitativas de corte transversal y de nivel descriptivo y correlacional. En el trabajo de campo se aplicó batería de preguntas para estudiantes y encuesta a docentes del área de matemáticas. Los resultados demuestran que el 76.9 % de los estudiantes tienen calificación menor o igual a seis puntos, lo que significa que no han superado los niveles de aprendizaje requeridos en la resolución de problemas. Los resultados de las encuestas a docentes muestran que el 80 % de ellos aplican herramientas tecnológicas y estrategias innovadoras, el 20 % utilizan las herramientas tecnológicas y videojuegos para mejorar sus enseñanzas. Se concluye que la lateralidad en los estudiantes colabora moderadamente a la seriación, identificación y comparación, la tecnología sirve como herramienta de gestión del conocimiento que favorece el aprendizaje, facilita la realización de tareas, favorecen la comunicación, investigación y la obtención de información.
Palabras clave: creatividad; estrategia didáctica; habilidad matemática; pensamiento lógico-matemático; resolución de problemas.
RESUMO
Segundo o último estudo do Instituto Nacional de Avaliação Educacional, o Equador está entre os países com maior dificuldade no desenvolvimento de competências e habilidades, com o nível mais baixo de conhecimento matemático (nem chegou ao nível 2). Por isso surge a necessidade de induzir os jovens a potencializar sua criatividade com o uso da lógica para resolver problemas matemáticos. Este artigo foi realizado para apresentar o resultado da construção de estratégias didáticas úteis no processo educacional da matemática, identificando as capacidades de resolução de problemas nos alunos da Unidade Educacional "Manuel Inocencio Parrales y Guale" do Cantão Jipijapa. Foi elaborado a partir de um delineamento não experimental com técnicas quantitativas de corte transversal e nível descritivo e correlacional. No trabalho de campo foi aplicada uma bateria de perguntas para os alunos e uma pesquisa com professores da área de matemática. Os resultados mostram que 76,9% dos alunos têm nota inferior ou igual a seis valores, o que significa que não ultrapassaram os níveis de aprendizagem exigidos na resolução de problemas. Os resultados das pesquisas com professores mostram que 80% de les aplicam ferramentas tecnológicas e estratégias inovadoras, 20% usam ferramentas tecnológicas e videogames para melhorar seus ensinos. Conclui-se que a lateralidade nos alunos contribui moderadamente para serialização, identificação e comparação, a tecnologia serve como ferramenta de gestão do conhecimento que favorece o aprendizado, facilita a realização de tarefas, favorece a comunicação, a pesquisa e a obtenção de informações.
Palavras-chave: criatividade; estratégia didática; habilidade matemática; pensamento lógico-matemático; resolução de problemas.
INTRODUCTION
Creative teaching strategies are a set of techniques and methods that teachers use in class to achieve their purpose. However, young people see a problem in mathematics, since teachers do not use adequate strategies; That is why they encounter difficulties in the development and management of skills. For this reason, student performance in mathematics is low. In this sense, it should be remembered that Ecuador is one of the countries with the most difficulties in this area and reflects a low level of knowledge of mathematics by children and adolescents.
In the work published by Cerda et al. (2017), it is argued that "Successful achievement and learning in mathematics continues to be a challenge worldwide, and great efforts are made to advance proposals for improvement that generally involve teachers in terms of their training, improvement or practice. classroom" (p. 1).
According to the study carried out by the National Institute for Educational Evaluation (INEVAL, 2018), the following is evidenced:
Serious difficulties of Ecuadorian students to function in situations that require the ability to solve mathematical problems. In the results of the 2018 PISA-D tests in which Ecuador participated for the first time, 70.9% of the students did not reach level 2 in mathematics, categorized as the basic performance level in mathematics, and failed the PISA test (p.44).
It is, therefore, a challenge that involves promoting creativity in students and the use and development of logic to solve mathematical problems.
For Mato et al. (2017) one of the objectives of the area of mathematics is: "that students are competent in solving problems, since their teaching is useful for daily life and significantly increases the learning of mathematical content" (p. 94).
Buitrago et al. (2020), who cited Leliwa et al. (2016), describes that "the teacher is a mediator between knowledge and the subject, a learning facilitator who designs strategies and activities based on the knowledge he wishes to teach" (p. 111). Therefore, the teacher must be the one who guides the processes so that the acquisition of knowledge of each student is effective and thus achieve mastery of the subject.
It is intended that students are able to solve problems and apply their study in the practice of the contents. For its part, Chuquihuanca et al. (2021) show that:
According to the United Nations Educational, Scientific and Cultural Organization (UNESCO) report, "higher education institutions should train students to become well-informed and deeply motivated citizens, endowed with a sense of critical and capable of analyzing society's problems, seeking solutions, applying them and assuming social responsibilities" (p. 17).
We live in a society in which rapid changes are taking place in the field of science and technology, so we have at our fingertips many tools and ways that help us solve the problems inherent in learning. For this, it is necessary to focus on the most appropriate recreational didactic strategies so that young people are able to solve problems and reach an optimal level of knowledge.
Problem solving is not only one of the purposes of teaching mathematics, but the essential means to achieve learning. Students should have opportunities to pose, explore and solve problems that require a significant effort (Ministry of Education, 2016, p. 53).
For their part, students must have the ability to solve mathematical problems, which entails acquiring greater intellectual potential to be self-sufficient and put into practice their reasoning skills and interpret mathematical problems assertively.
According to Gutiérrez et al. (2018), "didactic learning strategies represent the diversity of actions that the learner performs to strengthen the knowledge that the teacher teaches (...) and that are used to appreciate the achievement of the learning obtained by the student" (p. 39). Without a doubt, didactic strategies will be the driving force for students to achieve their specific learning.
According to Mato (2017), who quoted Beltrán (2003):
Mathematical activity is a process of construction of knowledge; In this discipline, one of the main interests of problem solving is the motivation caused by the problem itself (...). To solve mathematical problems, on the other hand, we need to develop certain strategies and apply them to a large number of situations (p. 94, 95).
For this reason, teachers must encourage students to instill in them the ability to think and reason from the relevant methods, techniques and strategies to enhance their skills.
According to the criteria of Van Dijk and Kintsch (1983), cited by Arrieta (2019) says: "in order to solve a certain mathematical problem, it is necessary to understand its semantic structure" (p. 21), which means that it is It is essential to interpret the exercise to arrive at the solution. Sharing the ideas of Van and Kintsch, it is really necessary to understand each mathematical exercise to arrive at the solution, since it is not simply a matter of trying to do it, but of analyzing each case or category to solve the problem.
Camarena (2017) states that "the methodological process of didactics is flexible and the teacher does not have to follow the steps as they are presented. Flexibility is what allows addressing different cultures, social levels and learning styles" (p. 17).
In this sense, it is necessary for the teacher to interact with the students and apply didactic methodologies with facts from reality, without leaving the topic being addressed. In the words of Breda et al. (2018): "effective teaching of mathematics requires students to understand what they know and what they need to learn, and therefore the challenge of supporting them in correct learning is posed" (p. 270).
All teaching is accompanied by challenges, since the study must be the strategic point of understanding in the student's practice to ensure meaningful learning.
This article proposes to socialize useful didactic strategies in the educational process of mathematics, identifying students' problem-solving abilities; In addition to raising awareness among teachers about the importance of applying creative teaching strategies that motivate and encourage students to seek solutions to the mathematical problems raised, improving the learning process in the area.
MATERIALS AND METHODS
This research work was developed from a non-experimental design with cross-sectional quantitative techniques and a descriptive and correlational level. The management of the variables was not compromised, but information was collected directly from the primary sources to determine the results that are expressed in the analysis of this article. It was of a cross-sectional nature, since a cut in time and a data collection that was compared with itself were taken as reference. It has a descriptive part with measures of central tendency for the explanation of the variables of the first study category (creative use of technology), while the second category (mathematical-logical thinking) was analyzed by means of central tendency calculations and correlations of the variables, calculated as dimensions of the study category.
The investigation took place in a public educational institution with morning and afternoon shifts located in the Jipijapa canton of the Manabí province. The student population was made up of 79 women and 116 men, legally enrolled in the Higher Basic Education sublevel of the institution, which, in turn, has five teachers in the area of mathematics in the sublevel chosen for the study. The student population underwent a simple random probabilistic sampling for the selection of participants. To calculate the sample size, the finite population sampling formula was applied, with a 5% margin of error and 95% confidence, with the participation of 130 subjects for the application of the instrument. Regarding the teaching staff, the sampling was intentional non-probabilistic, considering the distributive workload that was approved for the academic period 2021-2022, in which the study was carried out.
The instrument used in the first category was a structured basic survey with 11 questions aimed at exploring the use of technology from the beginning of creativity. The 11 survey variables were recalculated based on the answers for the interpretation of the data obtained.
Regarding the collection of information from the second category, a logical thinking assessment battery was used in the formal stage; This instrument consisted of six dimensions: seriation, classification, identification, laterality, correspondence, and comparison. Each dimension was divided into five graduated exercises to assess the level of maturity of the intellectual abilities required to solve problems in the formal thinking stage. The questionnaire was subjected to Cronbach's alpha coefficient, with which the overall score was 0.79, which determines an adequate degree of confidence in its structure. This test was applied to subjects between the ages of 12 and 15 or who are studying the level or grade corresponding to the sublevel of Higher Basic Education of the Ecuadorian National Education System.
The instrument is evaluated by dimensions on a scale from 1 to 10, with a mean point of approval equal to 7. The mean point has been determined based on the cumulative percentage that was calculated from the sample for validation. It is advisable to make comparisons of the means obtained by the subjects evaluated to establish significant differences between the sample groups.
Regarding the data analysis, the measures of central tendency were calculated and, in the case of the first category (creative use of technology), the relative frequency of the responses obtained from the application of the survey was quantified. An integrating variable was recalculated for the representation of the dimensions shown in graphs 1 and 2, as resulting from the variables included in it.
Regarding the second category, the variables are integrated into the dimensions evaluated by the instrument. In the first instance, the measures of central tendency of the global result of the scale (mean, mode, deviation, minimum, maximum and percentiles) were calculated. Then, the central tendencies of the results obtained by dimension were evaluated, to carry out a detailed analysis of the logical capacities that are stimulated from the methodology under study in this investigation.
Finally, the Pearson correlation was calculated on the results collected from the evaluable dimensions of the logical thinking scale. These data were used to determine the conclusions of the study and the relationships between the methodology applied for the research, the use of flowcharts and the logical thinking abilities that are involved in the mathematical learning of adolescents.
RESULTS
Creative teaching strategies
From an online survey applied to mathematics teachers in Higher Basic Education, results were obtained that enable understanding, the utility given to these strategies and their daily use in the teaching-learning process. Really, educating is provoking interest in learning in students, which results in motivation and, therefore, in carrying out activities to their full potential.
Results obtained in the survey carried out to teachers in the area of mathematics.
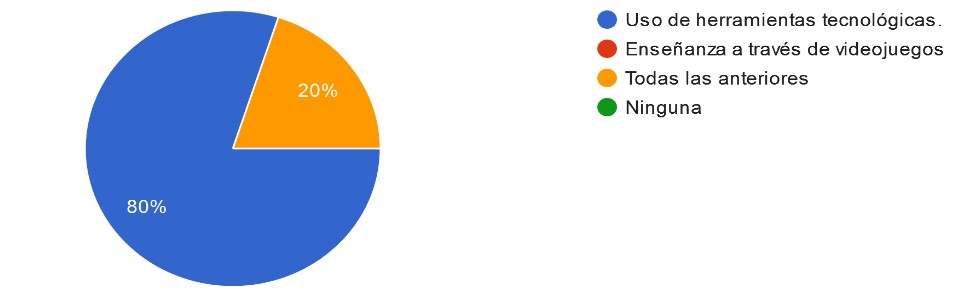
Graph. 1- Didactic tools used
Source: own elaboration , questions addressed to teachers of the mathematics area of the educational establishment and of other institutions
According to the statistically valued survey, referring to graph # 1, 80% of teachers apply technological tools as innovative strategies and 20% use technological tools and video games to improve their teachings.
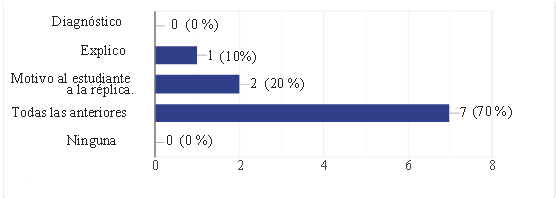
Graph. 2- Actions for creative and motivating practice
Source: own elaboration. Questions addressed to teachers of the mathematics area of the educational establishment and of other institutions
As revealed by the statistics reflected in graph # 2, 70% of the teachers carry out a diagnostic observation, explain and motivate the student to reply, while 20% only motivate to reply and 10% explain. Studies carried out on teachers show that a high percentage of them apply creative and motivating teaching strategies, although the results of the student survey show the opposite.
3.2. Consolidation of mathematical thought in the student body
online survey of students.
Table 1- Consolidated results of the logical thinking assessment battery in the formal stage.
No. |
Valid |
112 |
lost |
18 |
|
Half |
4.91 |
|
Fashion |
4.00 |
|
Dev . Standard |
2.64 |
|
Minimum |
0.00 |
|
Maximum |
9.67 |
|
percentiles |
25 |
3.33 |
50 |
4.67 |
|
75 |
6.67 |
|
Note: Equivalence is the average of the scores obtained in each dimension of the logical thinking battery.
The results obtained in the logical thinking assessment battery in the formal stage show that 76.9% of the student body has achieved a score equal to or less than 6.67. The average score of the students' performance is equivalent to 4.91 out of 10, with a standard deviation of 2.64, which implies that there is a wide distance between the scores obtained by the students in the instrument. The mode of the results is equal to 4.00, so they are in a performance percentile of less than 50%. The minimum grade achieved by the students is equivalent to 0.00 and the highest grade is 9.67, with which it could be inferred that there are students with high consolidation in their logical thinking for problem solving.
To complement the performance obtained from the global results of the application of the logical thinking battery, the scores by dimension that have been generated from the study are presented:
Table 2- Results by dimensions of the logical thinking battery in the formal stage
|
seriation |
ID |
Classification |
laterality |
Correspondence |
Comparison |
|
No. |
valid |
112 |
112 |
112 |
112 |
112 |
112 |
lost |
18 |
18 |
18 |
18 |
18 |
18 |
|
Half |
3.74 |
6.51 |
5.28 |
5.54 |
3.59 |
5.08 |
|
Fashion |
2.00 |
10.00 |
4.00 |
4.00 |
2.00 |
0.00 |
|
Dev . Standard |
2.39 |
3.72 |
3.19 |
3.39 |
3.12 |
3.49 |
|
Asymmetry |
0.75 |
-0.73 |
0.18 |
-0.06 |
0.58 |
-0.05 |
|
Note: There are multiple modes. The smallest value is displayed.
After having used the logical thinking battery in the formal stage, the results achieved by categories serve to visualize that the highest value was the identification dimension, in which an average of 6.51 was obtained, with a standard deviation of 3.72; in this case there is no normality in the distribution of the data. The values become unstable and the range between student groupings is very wide. For its part, the correspondence dimension is the lowest of all; in this, the mean is equal to 3.59 and its standard deviation is 3.12. Here, the data distribution does not conform to normality.
Table 3- Correlation of the dimensions of the logical thinking battery in the formal stage
|
seriation |
ID |
Classification |
laterality |
Correspondence |
Comparison |
seriation |
1 |
.346* |
.581** |
.518** |
.663** |
.475** |
ID |
.346* |
1 |
.661** |
.446** |
.554** |
.751** |
Classification |
.581** |
.661** |
1 |
.757** |
.678** |
.741** |
laterality |
.518** |
.446** |
.757** |
1 |
.729** |
.578** |
Correspondence |
.663** |
.554** |
.678** |
.729** |
1 |
.632** |
Comparison |
.475** |
.751** |
.741** |
.578** |
.632** |
1 |
Notes: *. The correlation is significant at the 0.05 level (one-sided).
**. The correlation is significant at the 0.01 level (one-sided). A correlation is strong if it is equal to or greater than 0.5.
The results obtained from the application of the logical thought battery in the formal stage, by virtue of the Pearson correlation test, show that the variables are strongly correlated. This could be interpreted as a collective strength in the logical thinking functions of the student body that has been evaluated.
Based on the data that have been generated from the primary sources of information, the graphs are presented to determine the normality of the distribution of the results:
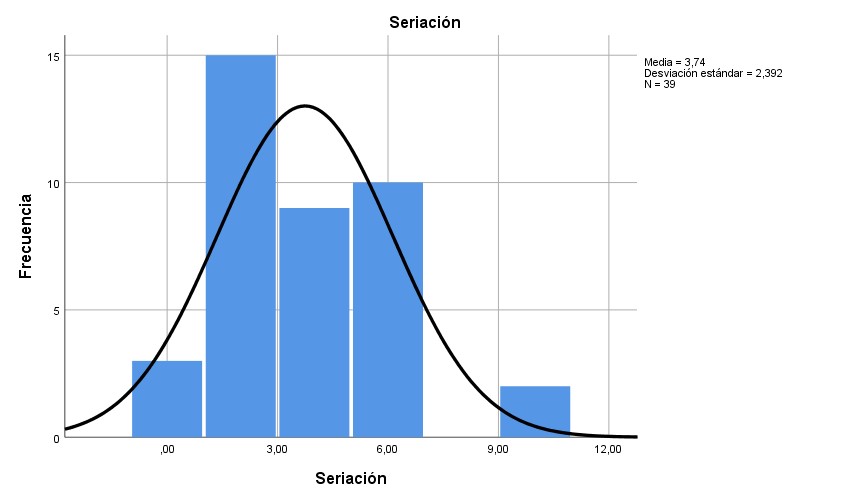
Graph. 3- Results of the seriation dimension
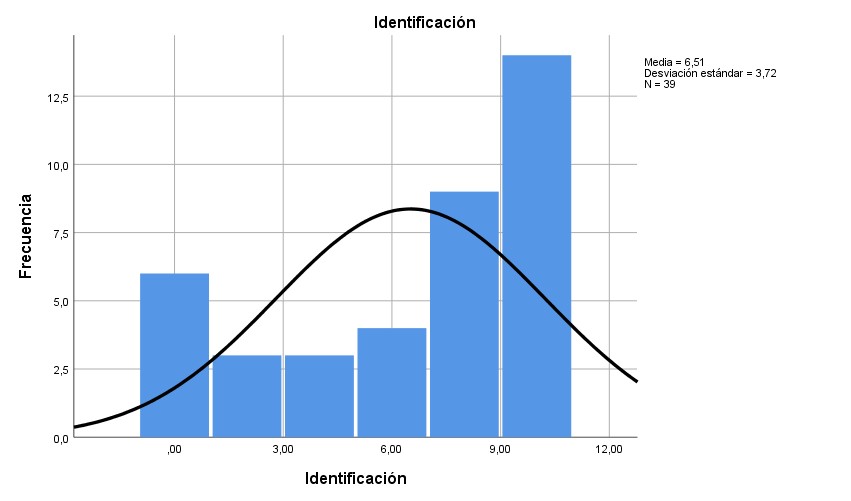
Graph. 4- Results of the identification dimension
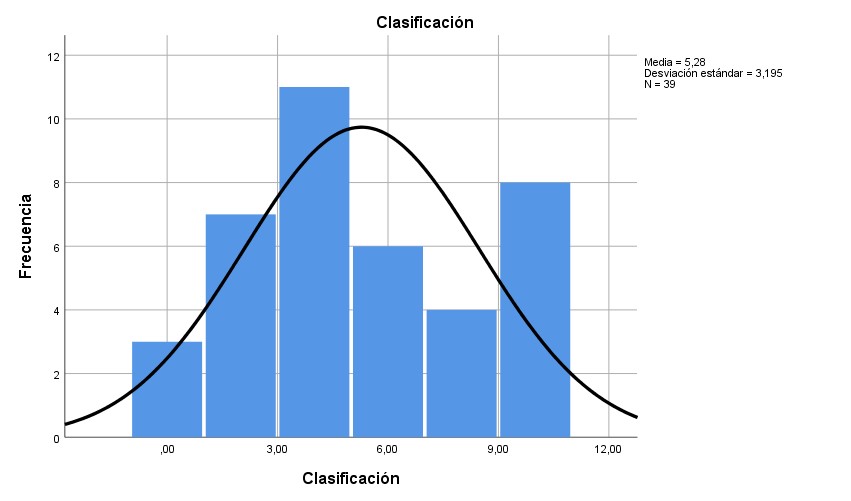
Graph. 5- Results of the classification dimension
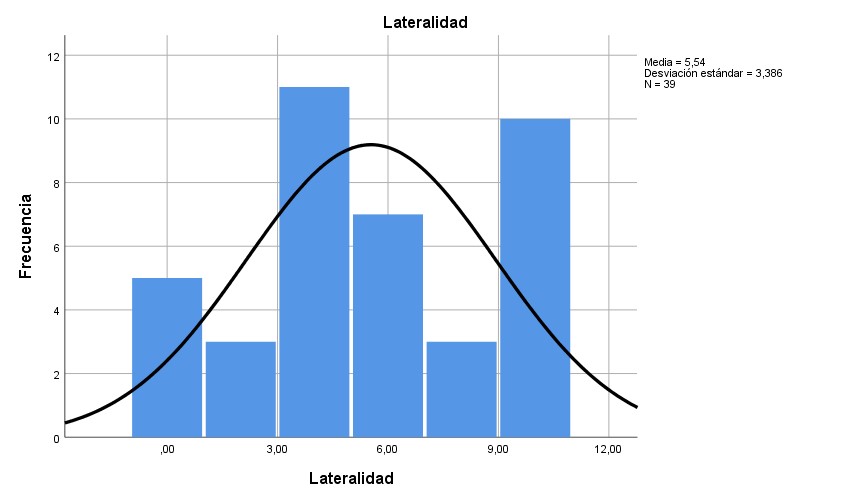
Graph. 6- Results of the laterality dimension
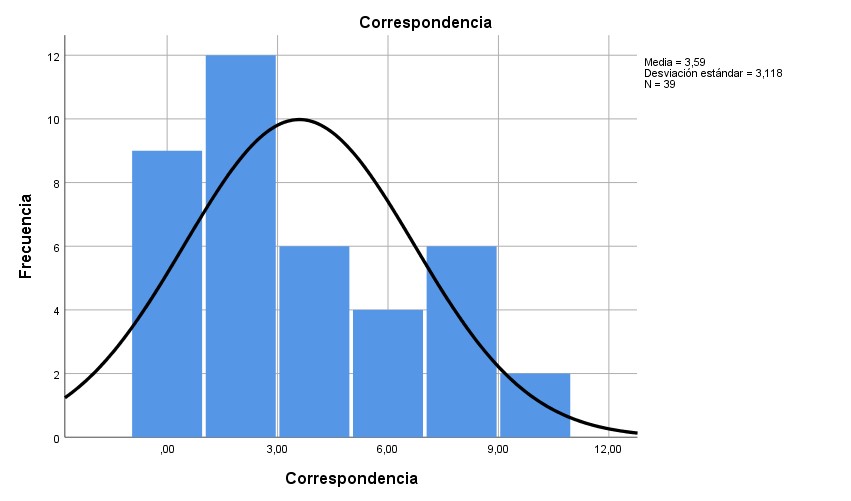
Graph. 7- Results of the correspondence dimension
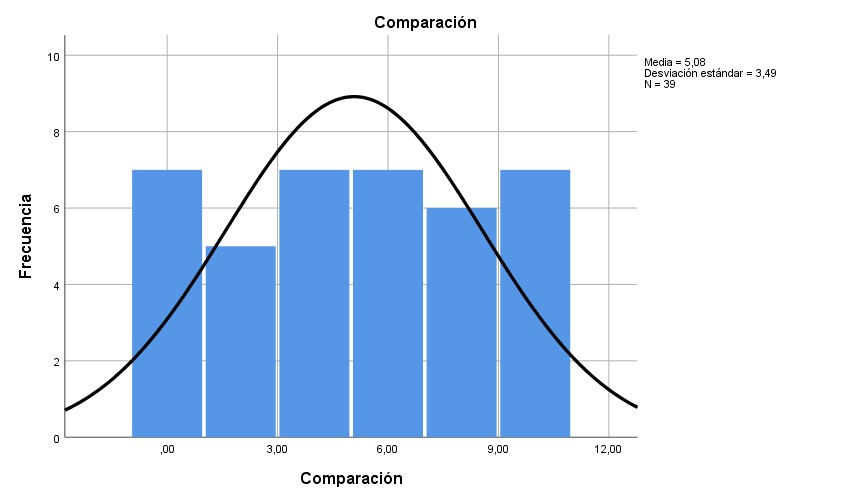
Graph. 8- Results of the comparison dimension
In the seriation dimension, 94.9% of those evaluated obtained scores equal to or less than 6 out of 10; In this case, the values are confirmed with the average mentioned in Table 2. In the identification dimension, the marker was greater than or equal to 8 in more than 64.1%. In the classification dimension, 69.2% of those evaluated reached scores equal to or less than 6. In the laterality dimension, 66.7% of the students evaluated had scores equal to or less than 6. In the correspondence dimension, 79.5% of those evaluated scored scores equal to or less than 6. In the comparison dimension, 82.1% received scores equal to or less than 8 points.
In graphs 1, 3, 4 and 6 it is verifiable that the distribution of these results is adjusted to normality, while in graphs 2 and 5 it is contemplated that the data is not distributed adjusted to normality.
DISCUSSION
From the studies carried out on teachers, it can be deduced that a high percentage of them resort to creative and motivating teaching strategies, while the results of the student survey show the opposite. In accordance with the contributions obtained, Cedeño et al. (2020) maintain that: "strategies should be designed in such a way that they encourage students to observe, analyze, comment, formulate hypotheses, seek solutions and discover knowledge for themselves" (p. 129).
The teacher must prepare his class using strategies that achieve the interest of the students. For this reason, "the didactics of mathematics should aspire to improve the functioning of the teaching and learning processes with criteria that allow them to be valued and guide their improvement" (Breda et al., 2018, p. 263).
It is essential that the teacher uses didactic material that contributes to improve the mathematical procedures of the students. On the other hand, "with the use of ICT, it is intended that students work autonomously so that they acquire knowledge and skills through the use of technology that allow them to function in society" (Montenegro et al., 2020, p. 316).
In this way, it is evident that technological tools help students to enhance their skills and, therefore, their academic performance.
Given what López (2017) stated, he states that:
When it comes to developing the creative potential of students, the teaching strategy is not alien to this way of acting, it is not a spontaneous act, much less mechanistic or simple (...). It is sought that teachers and students live in a creative learning environment, where mediations are generated that have creativity as their beginning, execution and purpose (p. 22).
The environment that surrounds, both teachers and students, must be harmonious to achieve good performance in students and a great satisfaction of profit in teachers.
According to Rodríguez (2007), cited by Benavidez and Flores (2019), "in the field of pedagogy, the educational strategy refers to the tasks and activities that teachers carry out systematically to achieve the specific learning objectives of a student "(p. 43). It is really important to have creative skills to promote student learning. In addition, "there can be no innovation without creativity, but the reverse does not happen, you can have characteristics of creativity and still never produce something innovative" (López, 2017, p. 13).
Before the application of the logical thinking battery in the formal stage to 79 women and 116 men, legally enrolled students of the educational institution, and after verifying their results achieved from the data from the students, the level of knowledge is revealed. of the students in the following categories: seriation, identification, classification, laterality, correspondence and comparison. The statistics show relevant data in each of the categories evaluated, where a lack in the development of logical thinking of the students can be evidenced. For this reason, teachers are asked to raise awareness about the importance of suitable strategies, techniques and instruments for learners, in order to increase the understanding of knowledge.
When the serialization task is stimulated in the didactic approach, it contributes moderately to the advancement of classification, laterality and comparison. However, exercising seriation directly encourages matching. In this case, when students are asked to order a series of data by common factors, the ability to classify symbols, numbers, or sets in mathematical language is induced. The use of technology facilitates teachers' access to Open Educational Resources (OER) to have online exercises at their fingertips for students to carry out serializations prior to classifying the symbols or elements that are available in the application.
Based on the data collected in the identification, it can be deduced that this moderately favors the increase in classification, laterality and correspondence. In this way, by exercising identification, comparison is directly encouraged. Currently, the use of technology helps young people to build skills such as creativity and independence, with which it is possible to see in them how technology can improve the learning experience.
From the data extracted in the Pearson correlation test, it is evident that, in the environment of the students, the classification helps moderately to promote the seriation and identification. However, exercising classification clearly drives progress in the dimensions of laterality, correspondence, and comparison. In reality, technology helps both students and teachers in all the activities they carry out in the educational field through educational programs and applications.
In the same way, in the laterality function in students, it is detected that it collaborates moderately with the seriation, identification and comparison function. Indeed, exercising laterality provides direct motivation in classification and correspondence. Information Technology and Communications (ICT) are highly recognized in the educational field by teachers and students, although they serve as knowledge management tools because they favor learning.
In the analysis of the table of functions in the students, it is reflected that the correspondence collaborates moderately in improving identification and comparison. Instead, it exercises correspondence, since it directly stimulates seriation, classification and laterality. The use of ICT or technological tools is essential in education, in the sense that they help and facilitate the tasks of the educational community. In addition, they favor communication, research and obtaining information.
Consequently, the students can detail the data obtained in the comparison function, which contributes moderately to the development of seriation, laterality and correspondence. However, exercising comparison serves to directly encourage identification and classification. With the use of new technological tools, teachers must be prepared and trained to contribute to productive school performance in students and thus improve interest in young people when carrying out their educational activities.
In the opinion of Moreno (2019), "serialization is a mental ability that allows establishing a relationship of order in a set of elements, taking into account both their similarities and differences" (p. 4).
BIBLIOGRAPHIC REFERENCES
Arrieta, M. (2019). Factores que inciden en el bajo rendimiento en el área de las matemáticas de los estudiantes de 8° de la institución educativa isla grande en el municipio de Sucre. 77. Trabajo de grado. Universidad Santo Tomas. Sucre. Col. http://bibliotecavirtualoducal.uc.cl:8081/handle/11634/18162.
Benavidez, V., & Flores, R. (2019). La importancia de las emociones para la neurodidáctica. Wimblu, Rev. Estud. de Psicología UCR, 14(1), 25-53. https://dialnet.unirioja.es/servlet/articulo?codigo=6794283
Breda, A., Font, V., & Pino, L. (2018). Criterios valorativos y normativos en la Didáctica de las Matemáticas: El caso del constructo idoneidad didáctica. Bolema: Boletim de Educação Matemática, 32(60), 255-278. https://doi.org/10.1590/1980-4415v32n60a13
Buitrago, I., Espinosa, N., & Martínez, J. (2020). Sentir y pensar el dominó como estrategia didáctica para aprender matemáticas. Voces y realidades educativas, 5, 109-118. http://vocesyrealidadeseducativas.com/volumen5/art_7.pdf
Camarena, P. G. (2017). Didáctica de la matemática en contexto. Educação Matemática Pesquisa, 19(2), https://doi.org/10.23925/1983-3156.2017v19i2p1-26
Cedeño, F., Chávez, J., & Parrales, Á. (2020). Estrategias didácticas para el aprendizaje de la multiplicación en las matemáticas en la educación en la educación general básica. Revista Cognosis, 5, 123-140. https://doi.org/10.33936/cognosis.v5i0.2782
Cerda, G., Pérez, C., Casas, J. A., & Ortega, R. (2017). Enseñanza y Aprendizaje de las Matemáticas: La necesidad de un análisis multidisciplinar. Psychology, Society & Education, 9(1), https://doi.org/10.21071/psye.v9i1.13848
Chuquihuanca, N., Fernández, M., Campoverde, G., Nieves, C., & Reyes, L. (2021). Material educativo gráfico: Una estrategia para desarrollar capacidades en el área de matemáticas Reyes Arteaga, L. Compas. Grupo de capacitación e investigación pedagógica. http://142.93.18.15:8080/jspui/bitstream/123456789/626/1/LIBRO_COMPAS.pdf
Gutiérrez-D, J., Gutiérrez-R, C., & Gutiérrez-R, J. (2018). Estrategias metodológicas de enseñanza y aprendizaje con un enfoque lúdico. Revista de Educación y Desarrollo, 45, 36-46.
INEVAL. (2018). Resultados de PISA para el desarrollo. INEVAL. Ecuador. https://www.evaluacion.gob.ec/wp-content/uploads/downloads/2018/12/CIE_InformeGeneralPISA18_20181123.pdf
López, R. (2017). Estrategias de enseñanza creativa. Investigaciones sobre la creatividad en el aula (Primera). Universidad de La Salle. http://biblioteca.clacso.edu.ar/Colombia/fce-unisalle/20180225093550/estrategiasen.pdf
Mato, D., Espiñeira, E., & López, V. A. (2017). Impacto del uso de estrategias metacognitivas en la enseñanza de las matemáticas. Perfiles educativos, 39(158), 91-111.
Ministerio de Educación. (2016). Currículo de EGB y BGU Matemática. Ministerio de Educación: Ecuador, https://educacion.gob.ec/wp-content/uploads/downloads/2016/03/MATE_COMPLETO.pdf
Montenegro, M., Muevecela, S., & Reinoso, M. (2020). Las Tics: Una nueva tendencia en la educación inclusiva. Revista Scientific, 5(17), 311-327.
Moreno, J. (2019). La seriación con habilidad mental para el desarrollo del pensamiento lógisto matemático en niños de 7 a 12 años. Universidad Técnica de Machala: Ecuador. http://repositorio.utmachala.edu.ec/bitstream/48000/14022/1/ECUACS_2019_EB_DE00011.pdf
Conflict of interests:
The author declares that she has no conflicts of interest.
Contribution of the authors:
The author participated in the design and writing of the work, and analysis of the documents.
![]()
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0
International License
Copyright (c) Salazar Reyes, J.