
Mendive. Revista de Educación, 21(1), e3230
Artículo original
Tecnología, creatividad y pensamiento lógico-matemático: una triada para repensar
Technology, creativity and logical-mathematical thinking: a triad to rethink
Tecnologia, criatividade e pensamento lógico-matemático: uma tríade para repensar
Emperatriz Salazar Reyes1![]() https://orcid.org/0000-0002-4200-4128
https://orcid.org/0000-0002-4200-4128
1 Universidad San Gregorio de Portoviejo, Manabí, Ecuador. ![]() jempesalar79@hotmail.com
jempesalar79@hotmail.com
| Salazar Reyes, J. (2023). Tecnología, creatividad y pensamiento lógico-matemático: una triada para repensar. Mendive. Revista de Educación, 21(1), e3230. https://mendive.upr.edu.cu/index.php/MendiveUPR/article/view/3230 |
Recibido: 20 de octubre 2022.
Aceptado: 30 de noviembre 2022.
RESUMEN
Según el último estudio del Instituto Nacional de Evaluación Educativa, Ecuador está entre los países con mayor dificultad en el desarrollo de destrezas y habilidades, con el nivel más bajo en conocimientos matemáticos (ni siquiera alcanzó el nivel 2). Es por eso que surge la necesidad de inducir a los jóvenes a impulsar su creatividad con el uso de la lógica para la resolución de problemas matemáticos. Este artículo se realizó para presentar el resultado de la construcción de estrategias didácticas útiles en el proceso educativo de las matemáticas, identificando las capacidades para la resolución de problemas en los estudiantes de la Unidad Educativa "Manuel Inocencio Parrales y Guale" del Cantón Jipijapa. Se elaboró a partir de un diseño no experimental con técnicas cuantitativas de corte transversal y de nivel descriptivo y correlacional. En el trabajo de campo se aplicó batería de preguntas para estudiantes y encuesta a docentes del área de matemáticas.Los resultados demuestran que el 76.9 % de los estudiantes tienen calificación menor o igual a seis puntos, lo que significa que no han superado los niveles de aprendizaje requeridos en la resolución de problemas. Los resultados de las encuestas a docentes muestran que el 80 % de ellos aplican herramientas tecnológicas y estrategias innovadoras, el 20 % utilizan las herramientas tecnológicas y videojuegos para mejorar sus enseñanzas. Se concluye que la lateralidad en los estudiantes colabora moderadamente a la seriación, identificación y comparación, la tecnología sirve como herramienta de gestión del conocimiento que favorece el aprendizaje, facilita la realización de tareas, favorecen la comunicación, investigación y la obtención de información.
Palabras clave: creatividad; estrategia didáctica; habilidad matemática; pensamiento lógico-matemático; resolución de problemas.
ABSTRACT
According to the latest study by the National Institute for Educational Evaluation, Ecuador is among the countries with the greatest difficulty in the development of skills and abilities, with the lowest level in mathematical knowledge (it did not even reach level 2). That is why the need arises to induce young people to boost their creativity with the use of logic to solve mathematical problems. This article was made to present the result of the construction of useful didactic strategies in the educational process of mathematics, identifying the problem-solving skills of students of the Manuel Inocencio Parrales y Guale Educational Unit of the Jipijapa Canton. It was elaborated from a non-experimental design with quantitative techniques of cross-sectional, descriptive and correlational level. In the field work, a battery of questions was applied to students and a survey to mathematics teachers. The results show that 76.9 % of the students have a grade lower or equal to six points, which means that they have not surpassed the required learning levels in problem solving. The results of the teacher surveys show that 80 % of them apply technological tools and innovative strategies, 20 % use technological tools and video games to improve their teaching. It is concluded that laterality in students collaborates moderately to seriation, identification and comparison, technology serves as a knowledge management tool that favors learning, facilitates the completion of tasks, favors communication, research and obtaining information.
Keywords: creativity; didactic strategy; mathematical ability; logical-mathematical thinking; problem solving.
RESUMO
Segundo o último estudo do Instituto Nacional de Avaliação Educacional, o Equador está entre os países com maior dificuldade no desenvolvimento de competências e habilidades, com o nível mais baixo de conhecimento matemático (nem chegou ao nível 2). Por isso surge a necessidade de induzir os jovens a potencializar sua criatividade com o uso da lógica para resolver problemas matemáticos. Este artigo foi realizado para apresentar o resultado da construção de estratégias didáticas úteis no processo educacional da matemática, identificando as capacidades de resolução de problemas nos alunos da Unidade Educacional "Manuel Inocencio Parrales y Guale" do Cantão Jipijapa. Foi elaborado a partir de um delineamento não experimental com técnicas quantitativas de corte transversal e nível descritivo e correlacional. No trabalho de campo foi aplicada uma bateria de perguntas para os alunos e uma pesquisa com professores da área de matemática. Os resultados mostram que 76,9% dos alunos têm nota inferior ou igual a seis valores, o que significa que não ultrapassaram os níveis de aprendizagem exigidos na resolução de problemas. Os resultados das pesquisas com professores mostram que 80% deles aplicam ferramentas tecnológicas e estratégias inovadoras, 20% usam ferramentas tecnológicas e videogames para melhorar seus ensinos. Conclui-se que a lateralidade nos alunos contribui moderadamente para serialização, identificação e comparação, a tecnologia serve como ferramenta de gestão do conhecimento que favorece o aprendizado, facilita a realização de tarefas, favorece a comunicação, a pesquisa e a obtenção de informações.
Palavras-chave: criatividade; estratégia didática; habilidade matemática; pensamento lógico-matemático; resolução de problemas.
INTRODUCCIÓN
Las estrategias didácticas creativas son un conjunto de técnicas y métodos que el profesorado emplea en la clase para alcanzar su propósito. Sin embargo, los jóvenes ven en las matemáticas un problema, puesto que los docentes no utilizan estrategias adecuadas; por eso se encuentran con dificultades en el desarrollo y manejo de destrezas. Por tal razón, el rendimiento del alumnado en matemáticas es bajo. En este sentido, cabe recordar que Ecuador es uno de los países con más dificultades en esta área y refleja un bajo nivel de conocimiento de las matemáticas por parte de niños, niñas y adolescentes.
En el trabajo publicado por Cerda et al. (2017), se argumenta que "El logro y aprendizaje exitoso en matemáticas sigue siendo un desafío a nivel mundial, y se realizan grandes esfuerzos para avanzar en propuestas de mejora que, generalmente, involucran al profesorado en términos de su formación, perfeccionamiento o práctica de aula" (p. 1).
De acuerdo con el estudio realizado por el Instituto Nacional de Evaluación Educativa (INEVAL, 2018), se evidencian:
Graves dificultades de los estudiantes ecuatorianos para desenvolverse en situaciones que requieren la capacidad de resolver problemas matemáticos. En los resultados de las pruebas PISA-D 2018 en las que Ecuador participó por primera vez, el 70.9 % de los estudiantes no alcanzó el nivel 2 en matemáticas, categorizado como el nivel de desempeño básico en matemáticas, y reprobó en la prueba PISA (p. 44).
Se trata, por tanto, de un desafío que implica promover en los estudiantes la creatividad y el uso y desarrollo de la lógica para la resolución de problemas matemáticos.
Para Mato et al. (2017) uno de los objetivos del área de matemáticas es: "que los alumnos sean competentes en la resolución de problemas, ya que su enseñanza tiene utilidad para la vida cotidiana e incrementa significativamente el aprendizaje de los contenidos matemáticos" (p. 94).
Buitrago et al. (2020), quien citó a Leliwa et al. (2016), describe que "el docente es un mediador entre el conocimiento y la materia, un facilitador del aprendizaje que diseña estrategias y actividades con base en los conocimientos que desea enseñar" (p. 111). Por tanto, el profesor debe ser quien oriente los procesos para que la adquisición de conocimientos de cada estudiante sea efectiva y así lograr el dominio de la asignatura.
Se pretende que los estudiantes sean capaces de resolver problemas y aplicar su estudio en la práctica de los contenidos. Por su parte, Chuquihuanca et al. (2021) demuestran que:
Según el informe de la Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (UNESCO), "las instituciones de educación superior deben formar a los estudiantes para que se conviertan en ciudadanos bien informados y profundamente motivados, provistos de un sentido crítico y capaces de analizar los problemas de la sociedad, buscar soluciones, aplicarlas y asumir responsabilidades sociales" (p. 17).
Vivimos en una sociedad en la que se están produciendo cambios acelerados en el ámbito de la ciencia y la tecnología, por lo que tenemos al alcance de la mano muchas herramientas y formas que nos ayudan a solucionar los problemas inherentes al aprendizaje. Para ello, es preciso enfocarse en las estrategias didácticas recreativas más adecuadas para que los jóvenes sean capaces de resolver problemas y alcanzar un óptimo nivel de conocimiento.
La resolución de problemas no es solo uno de los fines de la enseñanza de las matemáticas, sino el medio esencial para lograr el aprendizaje. Los estudiantes deberán tener las oportunidades de plantear, explorar y resolver problemas que requieran un esfuerzo significativo (Ministerio de Educación, 2016, p. 53).
Por su parte, los estudiantes deben contar con la capacidad para resolver problemas matemáticos, lo que conlleva adquirir mayor potencial intelectual para ser autosuficientes y poner en práctica sus habilidades de razonar e interpretar los problemas matemáticos de manera asertiva.
De acuerdo con Gutiérrez et al. (2018), "las estrategias didácticas de aprendizaje representan la diversidad de acciones que el aprendiz realiza para afianzar los conocimientos que el maestro enseña (…) y que se utilizan para apreciar el logro de los aprendizajes obtenidos por el alumno" (p. 39). Sin duda alguna, las estrategias didácticas serán el motor de guía en los estudiantes para alcanzar su aprendizaje específico.
Según Mato (2017), quien citó a Beltrán (2003):
La actividad matemática es un proceso de construcción del saber; en esta disciplina, uno de los principales intereses de la resolución de problemas es la motivación que provoca el propio problema (…). Para resolver los problemas matemáticos, por otro lado, necesitamos desarrollar determinadas estrategias y aplicarlas a un gran número de situaciones (p. 94, 95).
Por tal razón, los docentes deben estimular a los estudiantes para inculcar en ellos la capacidad de pensar y razonar a partir de los métodos, técnicas y estrategias pertinentes para potenciar sus habilidades.
Según criterios de Van Dijk y Kintsch (1983), citado por Arrieta (2019) dice: "para poder dar solución a determinado problema matemático, es necesario comprender la estructura semántica del mismo" (p. 21), lo que quiere decir que es imprescindible interpretar el ejercicio para llegar a la solución. Compartiendo ideas de Van y Kintsch, realmente es preciso comprender cada ejercicio matemático para llegar a la solución, pues no se trata simplemente de pretender hacer sino de analizar cada caso o categorías para resolver el problema.
Camarena (2017) manifiesta que "el proceso metodológico de la didáctica es flexible y el profesor no tiene por qué seguir los pasos tal cual se presentan. La flexibilidad es lo que permite abordar diversas culturas, niveles sociales y estilos de aprendizaje" (p. 17).
En este sentido, es preciso que el docente interactúe con los estudiantes y aplique metodologías didácticas con hechos de la realidad, sin salirse del tema que se aborda. En palabras de Breda et al. (2018): "una enseñanza efectiva de las matemáticas requiere que los estudiantes comprendan lo que conocen y lo que necesitan aprender, y por tanto se plantea el desafío de apoyarles en un aprendizaje correcto" (p. 270).
Toda enseñanza viene acompañada de desafíos y retos, puesto que el estudio debe ser el punto estratégico de comprensión en la práctica del alumno para asegurarse un aprendizaje significativo.
Este artículo propone socializar las estrategias didácticas útiles en el proceso educativo de las matemáticas, identificando las capacidades para la resolución de problemas de los estudiantes; además de concientizar a los docentes sobre la importancia de la aplicación de estrategias didácticas creativas, que motiven y estimulen a los estudiantes a buscar soluciones de los problemas matemáticos planteados mejorando el proceso de aprendizaje en el área.
MATERIALES Y MÉTODOS
Este trabajo de investigación se elaboró a partir de un diseño no experimental con técnicas cuantitativas de corte transversal y de nivel descriptivo y correlacional. No se comprometió el manejo de las variables, sino que se recogió información directamente de las fuentes primarias para la determinación de los resultados que se expresan en el análisis de este artículo. Fue de carácter transversal, por cuanto se tomó como referencia un corte en el tiempo y una recogida de datos que se comparó consigo misma. Posee una parte descriptiva con medidas de tendencia central para la explicación de las variables de la primera categoría de estudio (uso creativo de la tecnología), mientras que la segunda categoría (pensamiento-lógico matemático) se analizó mediante cálculos de tendencia central y correlaciones de las variables, calculadas como dimensiones de la categoría de estudio.
La investigación tuvo lugar en una institución educativa pública de jornada matutina y vespertina ubicada en el cantón Jipijapa de la provincia de Manabí. La población estudiantil estuvo compuesta por 79 mujeres y 116 hombres, legalmente matriculados en el subnivel de Educación Básica Superior de la institución que, a su vez, cuenta con cinco docentes del área de matemáticas en el subnivel elegido para el estudio. A la población estudiantil se le realizó un muestreo probabilístico aleatorio simple para la selección de los participantes. Para el cálculo del tamaño muestral se aplicó la fórmula de muestreo de poblaciones finitas, con un 5 % de margen de error y un 95 % de confianza, que contó con la participación de 130 sujetos para la aplicación del instrumento. Con relación al profesorado, el muestreo fue no probabilístico intencional, considerando el distributivo de carga horaria que se aprobó para el período académico 20212022, en que se realizó el estudio.
El instrumento que se empleó en la primera categoría fue una encuesta de base estructurada con 11 preguntas orientadas a la exploración del uso de la tecnología desde los principios de la creatividad. Las 11 variables de la encuesta se recalcularon en función de las contestaciones para la interpretación de los datos obtenidos.
En cuanto a la recogida de información de la segunda categoría se utilizó una batería de valoración de pensamiento lógico en etapa formal; ese instrumento constó de seis dimensiones: seriación, clasificación, identificación, lateralidad, correspondencia y comparación. Cada dimensión se dividió en cinco ejercicios graduados para valorar el nivel de madurez de las habilidades intelectuales requeridas para la resolución de problemas en el estadio del pensamiento formal. El cuestionario se sometió al coeficiente alfa de Cronbach, con lo que la puntuación global fue de 0.79, lo que determina un adecuado grado de confianza en su estructuración. Esta prueba se aplicó a sujetos de entre 12 y 15 años o que se encuentran cursando el nivel o grado correspondiente al subnivel de Educación Básica Superior del Sistema Nacional de Educación ecuatoriano.
El instrumento se valora por dimensiones en una escala de 1 a 10, con un punto medio de aprobación equivalente a 7. El punto medio se ha determinado en función del porcentaje acumulado que se calculó de la muestra para validación. Es recomendable realizar comparaciones de las medias obtenidas por los sujetos evaluados para establecer diferencias significativas entre los grupos muestrales.
Respecto al análisis de datos, se calcularon las medidas de tendencia central y, en el caso de la primera categoría (uso creativo de la tecnología), se cuantificó la frecuencia relativa de las respuestas obtenidas de la aplicación de la encuesta. Se procedió a recalcular una variable integradora para la representación de las dimensiones que se muestran en los gráficos 1 y 2, como resultantes de las variables incluidas en esta.
En lo relativo a la segunda categoría, las variables se integran en las dimensiones que evalúa el instrumento. En primera instancia, se calcularon las medidas de tendencia central del resultado global de la escala (media, moda, desviación, mínimo, máximo y percentiles). Luego, se evaluaron las tendencias centrales de los resultados obtenidos por dimensión, para realizar un análisis detallado de las capacidades lógicas que se estimulan desde la metodología sujeta a estudio en esta investigación.
Finalmente, se calculó la correlación de Pearson en los resultados recabados de las dimensiones evaluables de la escala de pensamiento lógico. Estos datos sirvieron para determinar las conclusiones del estudio y las relaciones existentes entre la metodología aplicada para la investigación, el uso de diagramas de flujo y las capacidades del pensamiento lógico que se involucran en el aprendizaje matemático de los adolescentes.
RESULTADOS
Estrategias didácticas creativas
A partir de una encuesta en línea aplicada a los docentes de matemáticas de la Educación Básica Superior se obtuvieron resultados que posibilitan la comprensión, la utilidad dada a estas estrategias y su uso cotidiano en el proceso de enseñanza-aprendizaje. Realmente, educar es provocar en los estudiantes el interés por aprender, lo que redunda en motivación y, por tanto, en la realización de actividades en su máximo potencial.
Resultados obtenidos en la encuesta realizada a docentes del área de matemáticas.
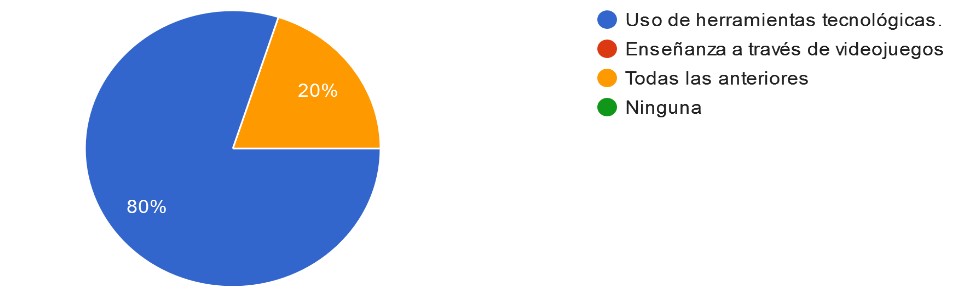
Gráf. 1- Herramientas didácticas utilizadas
Fuente: elaboración propia,preguntas dirigidas a docentes del área de matemáticas
del plantel educativo y de otras instituciones
De acuerdo con la encuesta valorada estadísticamente, referente al gráfico # 1, el 80 % de los docentes aplican herramientas tecnológicas como estrategias innovadoras y el 20 % utilizan las herramientas tecnológicas y videojuegos para mejorar sus enseñanzas.
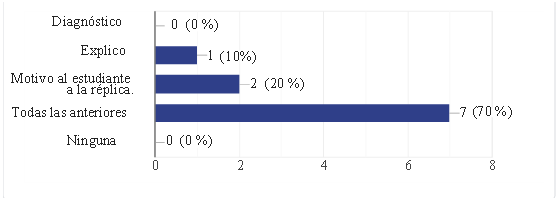
Gráf. 2- Acciones para la práctica creativa y motivadora
Fuente: elaboración propia.Preguntas dirigidas a docentes del área de matemáticas
del plantel educativo y de otras instituciones
Según revelan las estadísticas que refleja el gráfico # 2, el 70 % de los docentes llevan a cabo una observación diagnóstica, explican y motivan al estudiante a la réplica, mientras que el 20 % solo motiva a replicar y el 10 % explica. Estudios realizados a docentes reflejan que un alto porcentaje de ellos aplican estrategias didácticas creativas y motivadoras, aunque los resultados de la encuesta a estudiantes demuestran lo contrario.
3.2. Consolidación del pensamiento matemático en el estudiantado
La tabla 1 detalla los datos obtenidos de los instrumentos de evaluación que se aplicaron en esta investigación, mediante una encuesta realizada a estudiantes vía online.
Tabla 1-Resultados consolidados de la batería de valoración del pensamiento lógico en etapa formal.
N |
Válido |
112 |
Perdidos |
18 |
|
Media |
4.91 |
|
Moda |
4.00 |
|
Desv. Estándar |
2.64 |
|
Mínimo |
0.00 |
|
Máximo |
9.67 |
|
Percentiles |
25 |
3.33 |
50 |
4.67 |
|
75 |
6.67 |
|
Nota: la equivalencia es el promedio de los puntajes obtenidos en cada dimensión de la batería de pensamiento lógico.
Los resultados obtenidos en la batería de valoración del pensamiento lógico en etapa formal muestran que el 76.9 % del estudiantado ha logrado igual o menor puntaje que 6.67. El puntaje medio del rendimiento de los estudiantes equivale 4.91 sobre 10, con una desviación estándar de 2.64, lo que implica que existe amplia distancia entre los puntajes obtenidos por los estudiantes en el instrumento. La moda de los resultados equivale a 4.00, por lo que se encuentran en un percentil de rendimiento menor al 50 %. La nota mínima alcanzada por los estudiantes equivale a 0.00 y la mayor calificación es de 9.67, con lo que se podría inferir que existen estudiantes con alta consolidación en su pensamiento lógico para la resolución de problemas.
Para complementar los desempeños obtenidos desde los resultados globales de la aplicación de la batería de pensamiento lógico se presentan los puntajes por dimensión que se han generado a partir del estudio:
Tabla 2- Resultados por dimensiones de la batería de pensamiento lógico en etapa formal
|
Seriación |
Identificación |
Clasificación |
Lateralidad |
Correspondencia |
Comparación | |
N |
Válidos |
112 |
112 |
112 |
112 |
112 |
112 |
Perdidos |
18 |
18 |
18 |
18 |
18 |
18 |
|
Media |
3.74 |
6.51 |
5.28 |
5.54 |
3.59 |
5.08 |
|
Moda |
2.00 |
10.00 |
4.00 |
4.00 |
2.00 |
0.00 |
|
Desv. Estándar |
2.39 |
3.72 |
3.19 |
3.39 |
3.12 |
3.49 |
|
Asimetría |
0.75 |
-0.73 |
0.18 |
-0.06 |
0.58 |
-0.05 |
|
Nota: existen múltiples modos. Se muestra el valor más pequeño.
Luego de haber utilizado la batería de pensamiento lógico en etapa formal, los resultados alcanzados por categorías sirven para visualizar que la mayor valoración fue la dimensión de identificación, en la que se obtuvo una media de 6.51, con una desviación estándar de 3.72; en este caso no hay normalidad en la distribución de los datos. Los valores se vuelven inestables y el rango entre las agrupaciones de estudiantes es muy amplio. Por su parte, la dimensión correspondencia es la más baja de todas; en esta, la media equivale a 3.59 y su desviación estándar es 3.12. Aquí, la distribución de datos no se ajusta a la normalidad.
Tabla 3- Correlación de las dimensiones de la batería de pensamiento lógico en etapa formal
|
Seriación |
Identificación |
Clasificación |
Lateralidad |
Correspondencia |
Comparación |
Seriación |
1 |
.346* |
.581** |
.518** |
.663** |
.475** |
Identificación |
.346* |
1 |
.661** |
.446** |
.554** |
.751** |
Clasificación |
.581** |
.661** |
1 |
.757** |
.678** |
.741** |
Lateralidad |
.518** |
.446** |
.757** |
1 |
.729** |
.578** |
Correspondencia |
.663** |
.554** |
.678** |
.729** |
1 |
.632** |
Comparación |
.475** |
.751** |
.741** |
.578** |
.632** |
1 |
Notas: *. La correlación es significativa en el nivel 0.05 (unilateral).
**. La correlación es significativa en el nivel 0.01 (unilateral). Una correlación es fuerte si es igual o mayor que 0.5.
Los resultados obtenidos de la aplicación de la batería de pensamiento lógico en etapa formal, en virtud de la prueba de correlación de Pearson, demuestran que las variables se correlacionan fuertemente. Esto podría interpretarse como una fortaleza colectiva en las funciones del pensamiento lógico del estudiantado que ha sido evaluado.
Con base en los datos que se han generado a partir de las fuentes primarias de información, se presentan los gráficos para determinar la normalidad de la distribución en los resultados:
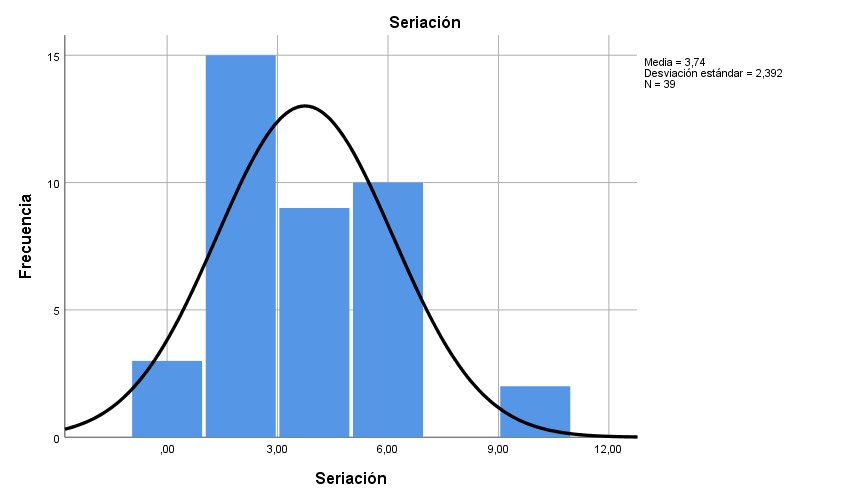
Gráf. 3- Resultados de la dimensión de seriación
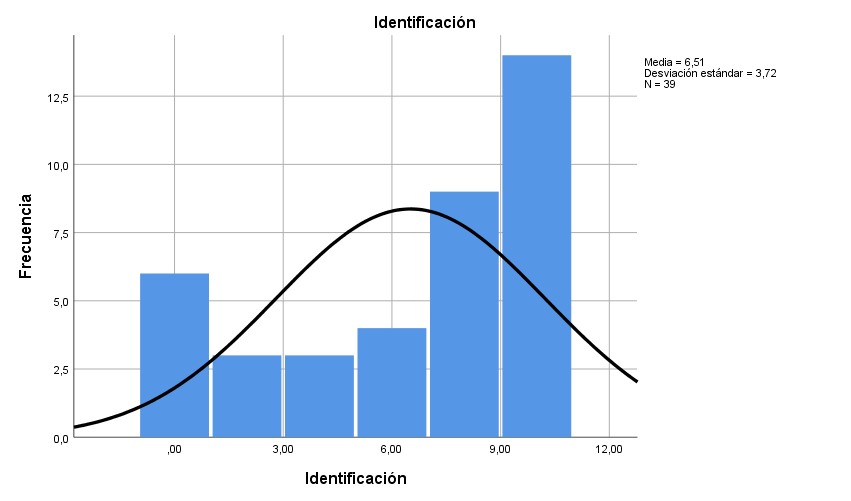
Gráf. 4- Resultados de la dimensión de identificación
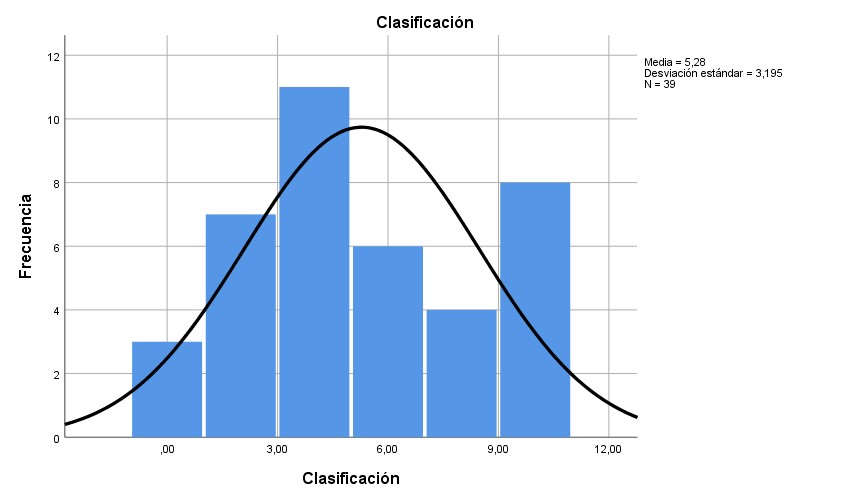
Gráf. 5- Resultados de la dimensión de clasificación
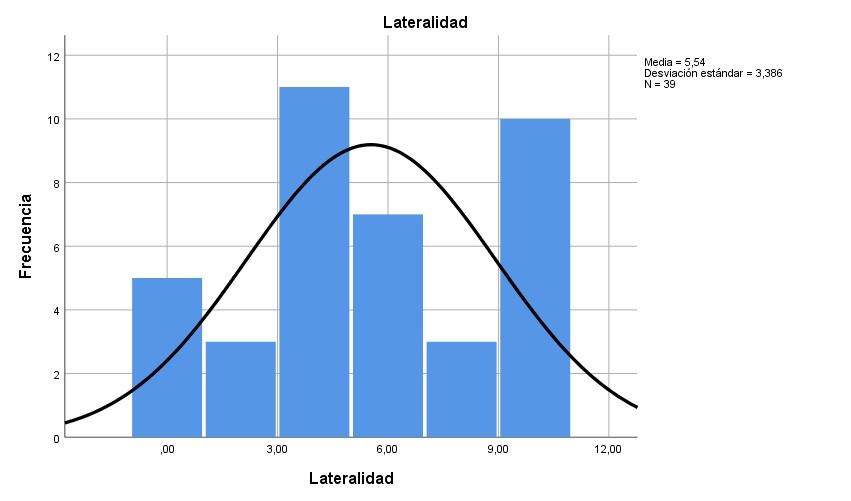
Gráf. 6- Resultados de la dimensión de lateralidad
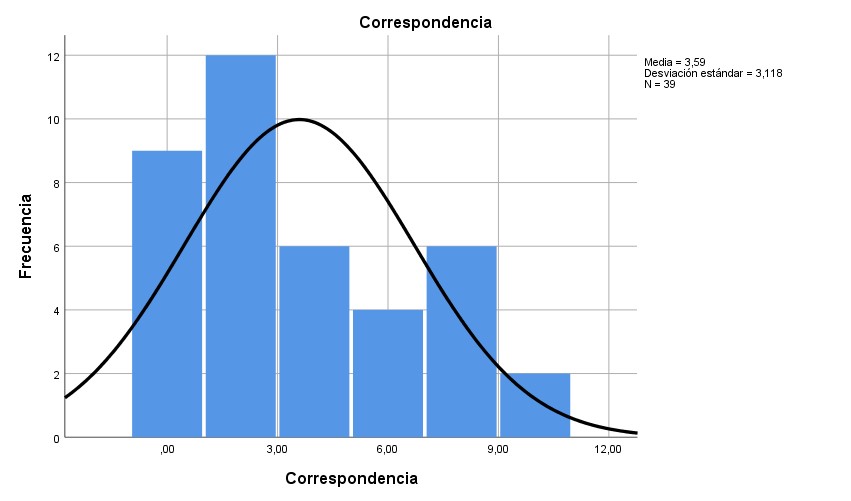
Gráf. 7- Resultados de la dimensión de correspondencia
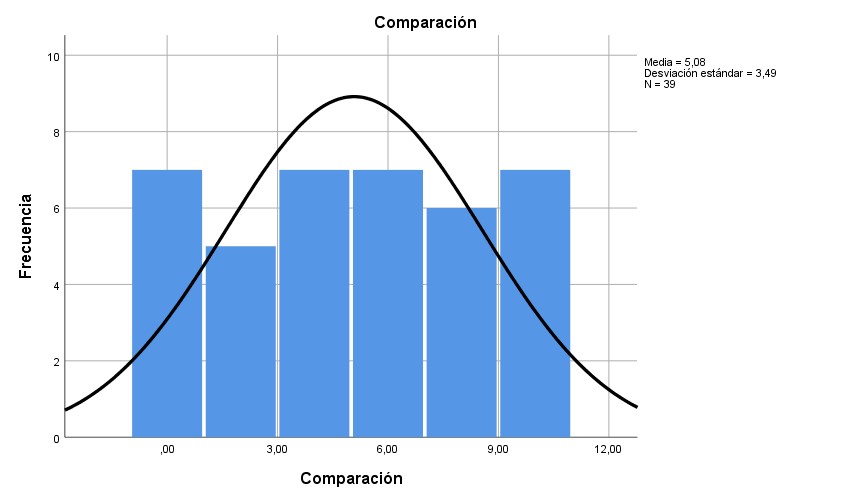
Gráf. 8- Resultados de la dimensión de comparación
En la dimensión de seriación, el 94.9 % de los evaluados obtuvo puntajes iguales o menores que 6 sobre 10; en este caso, los valores se ratifican con el promedio mencionado en la tabla 2. En la dimensión de identificación, el marcador fue mayor o igual que 8 en más del 64.1 %. En la dimensión de clasificación, el 69.2 % de los evaluados alcanzó puntajes iguales o menores que 6. En la dimensión de lateralidad, el 66.7 % de los estudiantes evaluados tuvieron puntajes iguales o menores a 6. En la dimensión de correspondencia, el 79.5 % de los evaluados anotó puntuaciones iguales o menores que 6. En la dimensión de comparación, el 82.1 % recibió calificaciones iguales o menores que 8 puntos.
En los gráficos 1, 3, 4 y 6 es comprobable que la distribución de estos resultados se ajusta a la normalidad, al tiempo que en los gráficos 2 y 5 se contempla que los datos no se distribuyen ajustados a la normalidad.
DISCUSIÓN
De los estudios realizados a docentes se desprende que un alto porcentaje de ellos recurren a estrategias didácticas creativas y motivadoras, mientras que los resultados de la encuesta a estudiantes demuestran lo contrario. En concordancia con los aportes obtenidos, Cedeño et al. (2020) sostienen que: "las estrategias deben ser diseñadas de modo que estimulen a los estudiantes a observar, analizar, opinar, formular hipótesis, buscar soluciones y descubrir el conocimiento por sí mismos" (p. 129).
El docente debe preparar su clase utilizando estrategias que logren el interés de los estudiantes. Por eso, "la didáctica de las matemáticas debe aspirar a la mejora del funcionamiento de los procesos de enseñanza y aprendizaje con criterios que permitan valorarlos y guiar su mejora" (Breda et al., 2018, p. 263).
Es fundamental que el docente utilice material didáctico que contribuya a mejorar los procedimientos matemáticos de los estudiantes. Por otra parte, "con el uso de las TIC se pretende que los estudiantes trabajen de manera autónoma para que adquieran conocimientos y habilidades mediante el uso de la tecnología que les permitan desenvolverse en la sociedad" (Montenegro et al., 2020, p. 316).
De esta forma, es evidente que las herramientas tecnológicas ayudan al estudiante a potenciar sus destrezas y, por tanto, su rendimiento académico.
Ante lo expuesto por López (2017) manifiesta que:
Cuando se trata de desarrollar el potencial creativo de los estudiantes, la estrategia de enseñanza no es ajena a esa forma de actuar, no es un acto espontáneo ni mucho menos mecanicista o simple (…). Se busca que profesores y estudiantes vivan en un ambiente de aprendizaje creativo, en donde se generen mediaciones que tengan por inicio, ejecución y finalidad la creatividad (p. 22).
El entorno que rodea, tanto a docentes como a estudiantes, debe ser armónico para lograr un buen rendimiento en los estudiantes y una gran satisfacción de provecho en los docentes.
Según Rodríguez (2007), citado por Benavidez y Flores (2019), "en el campo de la pedagogía, la estrategia educativa se refiere a las tareas y actividades que los docentes realizan de manera sistemática para lograr los objetivos de aprendizaje específicos de un alumno" (p. 43). Es realmente importante tener habilidades creativas para favorecer el aprendizaje de los estudiantes. Además, "no puede haber innovación sin creatividad, pero no ocurre a la inversa, se puede llegar a tener características propias de la creatividad y aun así jamás producir algo innovador" (López, 2017, p. 13).
Antes de la aplicación de la batería de pensamiento lógico en etapa formal a 79 mujeres y 116 hombres, estudiantes legalmente matriculados de la institución educativa, y después de comprobar sus resultados alcanzados a partir de los datos procedentes de los estudiantes se revela el nivel de conocimiento de los educandos en las siguientes categorías: seriación, identificación, clasificación, lateralidad, correspondencia y comparación. La estadística muestra datos relevantes en cada una de las categorías evaluadas, donde se puede evidenciar carencia en el desarrollo del pensamiento lógico de los estudiantes. Por esta razón, se pide a los docentes concientizar acerca de la importancia de las estrategias, técnicas e instrumentos idóneos para los aprendices, con el fin de acrecentar la comprensión de los conocimientos.
Cuando en el abordaje didáctico se estimula el cometido de seriación, esta colabora medianamente en el avance de la clasificación, lateralidad y comparación. Sin embargo, ejercitar la seriación fomenta directamente la correspondencia. En este caso, cuando se le pide al estudiantado que ordene una serie de datos por factores comunes, a su vez se induce la capacidad de clasificar símbolos, números o conjuntos en el lenguaje matemático. El uso de la tecnología facilita el acceso del profesorado a los Recursos Educativos Abiertos (REA) para tener a su alcance ejercicios en línea para que los estudiantes realicen seriaciones de forma previa a la clasificación de los símbolos o elementos que se encuentran disponibles en la aplicación.
A tenor de los datos recopilados en la identificación, se deduce que esta favorece medianamente el incremento de la clasificación, lateralidad y correspondencia. De esta forma, al ejercitar la identificación se incentiva directamente la comparación. En la actualidad, el uso de la tecnología ayuda a los jóvenes a construir habilidades como la creatividad e independencia, con lo que se logra ver en ellos cómo la tecnología puede mejorar la experiencia de aprendizaje.
A partir de los datos extraídos en la prueba de correlación de Pearson se evidencia que, en el entorno de los estudiantes, la clasificación ayuda medianamente a propiciar la seriación e identificación. No obstante, ejercitar la clasificación impulsa claramente el progreso de las dimensiones de lateralidad, correspondencia y comparación. En realidad, la tecnología ayuda, tanto a estudiantes como a docentes, en todas las actividades que ejecutan en el ámbito educativo por medio de programas y aplicaciones educativas.
De igual manera, en la función de lateralidad en los estudiantes se detecta que esta colabora medianamente a la función seriación, identificación y comparación. En efecto, ejercitar la lateralidad aporta una motivación directa en la clasificación y la correspondencia. Las Tecnologías de la Informática y las Comunicaciones (TIC) son muy reconocidas en el ámbito educativo por docentes y estudiantes, si bien sirven como herramientas de gestión del conocimiento porque favorecen el aprendizaje.
En el análisis de la tabla de funciones en los alumnos se refleja que la correspondencia colabora medianamente en mejora de la identificación y la comparación. En cambio, ejercita la correspondencia, puesto que estimula directamente la seriación, clasificación y lateralidad. El uso de las TIC o herramientas tecnológicas es fundamental en la educación, en el sentido de que ayudan y facilitan las tareas de la comunidad educativa. Además, favorecen la comunicación, la investigación y la obtención de información.
En consecuencia, en los estudiantes se pueden detallar los datos obtenidos en la función de comparación, la cual contribuye medianamente al desarrollo de la seriación, lateralidad y correspondencia. Sin embargo, ejercitar la comparación sirve para alentar directamente la identificación y clasificación. Con el uso de las nuevas herramientas tecnológicas los docentes deben prepararse y capacitarse para aportar al rendimiento escolar productivo en los estudiantes y así mejorar el interés en los jóvenes al momento de efectuar sus actividades educativas.
A juicio de Moreno (2019), "la seriación es una habilidad mental que permite establecer una relación de orden en un conjunto de elementos, tomando en consideración tanto sus semejanzas como diferencias" (p. 4).
REFERENCIAS BIBLIOGRÁFICAS
Arrieta, M. (2019). Factores que inciden en el bajo rendimiento en el área de las matemáticas de los estudiantes de 8° de la institución educativa isla grande en el municipio de Sucre. 77. Trabajo de grado. Universidad Santo Tomas. Sucre. Col. http://bibliotecavirtualoducal.uc.cl:8081/handle/11634/18162.
Benavidez, V., & Flores, R. (2019). La importancia de las emociones para la neurodidáctica. Wimblu, Rev. Estud. de Psicología UCR, 14(1), 25-53. https://dialnet.unirioja.es/servlet/articulo?codigo=6794283
Breda, A., Font, V., & Pino, L. (2018). Criterios valorativos y normativos en la Didáctica de las Matemáticas: El caso del constructo idoneidad didáctica. Bolema: Boletim de Educação Matemática, 32(60), 255-278. https://doi.org/10.1590/1980-4415v32n60a13
Buitrago, I., Espinosa, N., & Martínez, J. (2020). Sentir y pensar el dominó como estrategia didáctica para aprender matemáticas. Voces y realidades educativas, 5, 109-118. http://vocesyrealidadeseducativas.com/volumen5/art_7.pdf
Camarena, P. G. (2017). Didáctica de la matemática en contexto. Educação Matemática Pesquisa, 19(2), https://doi.org/10.23925/1983-3156.2017v19i2p1-26
Cedeño, F., Chávez, J., & Parrales, Á. (2020). Estrategias didácticas para el aprendizaje de la multiplicación en las matemáticas en la educación en la educación general básica. Revista Cognosis, 5, 123-140. https://doi.org/10.33936/cognosis.v5i0.2782
Cerda, G., Pérez, C., Casas, J. A., & Ortega, R. (2017). Enseñanza y Aprendizaje de las Matemáticas: La necesidad de un análisis multidisciplinar. Psychology, Society & Education, 9(1), https://doi.org/10.21071/psye.v9i1.13848
Chuquihuanca, N., Fernández, M., Campoverde, G., Nieves, C., & Reyes, L. (2021). Material educativo gráfico: Una estrategia para desarrollar capacidades en el área de matemáticas Reyes Arteaga, L. Compas. Grupo de capacitación e investigación pedagógica. http://142.93.18.15:8080/jspui/bitstream/123456789/626/1/LIBRO_COMPAS.pdf
Gutiérrez-D, J., Gutiérrez-R, C., & Gutiérrez-R, J. (2018). Estrategias metodológicas de enseñanza y aprendizaje con un enfoque lúdico. Revista de Educación y Desarrollo, 45, 36-46.
INEVAL. (2018). Resultados de PISA para el desarrollo. INEVAL. Ecuador. https://www.evaluacion.gob.ec/wp-content/uploads/downloads/2018/12/CIE_InformeGeneralPISA18_20181123.pdf
López, R. (2017). Estrategias de enseñanza creativa. Investigaciones sobre la creatividad en el aula (Primera). Universidad de La Salle. http://biblioteca.clacso.edu.ar/Colombia/fce-unisalle/20180225093550/estrategiasen.pdf
Mato, D., Espiñeira, E., & López, V. A. (2017). Impacto del uso de estrategias metacognitivas en la enseñanza de las matemáticas. Perfiles educativos, 39(158), 91-111.
Ministerio de Educación. (2016). Currículo de EGB y BGU Matemática. Ministerio de Educación: Ecuador, https://educacion.gob.ec/wp-content/uploads/downloads/2016/03/MATE_COMPLETO.pdf
Montenegro, M., Muevecela, S., & Reinoso, M. (2020). Las Tics: Una nueva tendencia en la educación inclusiva. Revista Scientific, 5(17), 311-327.
Moreno, J. (2019). La seriación con habilidad mental para el desarrollo del pensamiento lógisto matemático en niños de 7 a 12 años. Universidad Técnica de Machala: Ecuador. http://repositorio.utmachala.edu.ec/bitstream/48000/14022/1/ECUACS_2019_EB_DE00011.pdf
Conflicto de intereses:
La autora declara no tener conflictos de intereses.
Contribución de los autores:
La autora participó en el diseño y redacción del trabajo, y análisis de los documentos.
![]()
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial 4.0 Internacional
Copyright (c) Salazar Reyes, J.