Didactic activities for learning about the location of ordered pairs in the Cartesian plane

Didactic activities for learning about the location of ordered pairs in the Cartesian plane

Actividades didácticas para el aprendizaje sobre la ubicación de pares ordenados en el plano cartesiano

Atividades didáticas para aprendizado da localização de pares ordenados no plano cartesiano

¹Pontifical Catholic University of Ecuador, Santo Domingo headquarters. Ecuador pdcedenoh@pucesd.edu.ec; rlorenzo@pucesd.edu.ec; mdloaizac@pucesd.edu.ec

**Citar como**
Cedeño Heras, P., Lorenzo Benítez, R., & Loaiza Castillo, M. (2023). Didactic activities for learning about the location of ordered pairs in the Cartesian plane. Mendive. Revista de Educación, 21(1), e3129. https://mendive.upr.edu.cu/index.php/MendiveUPR/article/view/3129

This research is interested in topics of vital importance in the study of Mathematics. Therefore, it is necessary to describe the level of knowledge that students have about the location of ordered pairs in the Cartesian plane with natural numbers, in order to make decisions that favor quality education. The approach taken was quantitative, with a non-experimental design and a descriptive scope in terms of the type of research. The sample and the population are identical, 15 6th grade ^EGBstudents from the "Julio Moreno Espinosa" Educational Unit. For data collection, the survey was used as a technique and the questionnaire as an instrument. The analysis of the results with descriptive statistics and SPSS allowed us to understand the level of knowledge of the students according to the established indicators and in a general way. It could be seen that, although 13.3% of those evaluated are at a low level, the majority are at a medium level and 40.0% are at a high level. The most affected indicator was information processing. From this, a proposal was conceived that will improve the situation that affects students so that they can achieve better school performance. It also favors teachers, because it invites them to work in a more dynamic way in the area of mathematics.

Esta investigación se interesa por temas de vital importancia en el estudio de las Matemáticas. Por lo tanto, es necesario describir cómo es el nivel de conocimiento que tienen los estudiantes sobre la ubicación de pares ordenados en el plano cartesiano con números naturales, para tomar decisiones que favorezcan a una educación de calidad. El enfoque asumido fue el cuantitativo, con un diseño no experimental y un alcance descriptivo en cuanto al tipo de investigación. La muestra y la población son idénticas, 15 estudiantes de 6to grado de EGB de la Unidad Educativa "Julio Moreno Espinosa". Para la recolección de datos se empleó la encuesta como técnica y el cuestionario como instrumento. El análisis de los resultados con estadística descriptiva y SPSS permitió comprender el nivel de conocimiento de los estudiantes según los indicadores establecidos y de forma general. Se pudo apreciar que, aunque el 13,3 % de los evaluados se encuentra en un nivel bajo, la mayoría se ubica en un nivel medio y el 40,0 % está en nivel alto. El indicador más afectado fue el procesamiento de la información. A partir de esto se concibió una propuesta que permitirá mejorar la situación que afecta a los estudiantes para que consiga un mejor desempeño escolar. También favorece a los docentes, porque invita a trabajar de una forma más dinámica en el área de las matemáticas.

Esta pesquisa está interessada em tópicos de vital importância no estudo da Matemática. Portanto, é necessário descrever o nível de conhecimento que os alunos têm sobre a localização dos pares ordenados no plano cartesiano com os números naturais, a fim de tomar decisões que favoreçam o ensino de qualidade. A abordagem adotada foi quantitativa, com delineamento não experimental e escopo descritivo quanto ao tipo de pesquisa. A amostra e a população são idênticas, 15 alunos do 6º ano da EGB da Unidade Educacional "Julio Moreno Espinosa". Para a coleta de dados, utilizou-se o survey como técnica e o questionário como instrumento. A análise dos resultados com estatística descritiva e SPSS permitiu compreender o nível de conhecimento dos alunos segundo os indicadores estabelecidos e de forma geral. Pôde-se constatar que, embora 13,3% dos avaliados estejam em nível baixo, a maioria está em nível médio e 40,0% em nível alto. O indicador mais afetado foi o processamento da informação. A partir disso, foi concebida uma proposta que irá melhorar a situação que afeta os alunos para que eles possam alcançar um melhor desempenho escolar. Também favorece os professores, pois os convida a trabalhar de forma mais dinâmica na área da matemática.

Teaching assumes a great challenge today and teachers in Latin America, including Ecuador, do not escape it. The Teaching-Learning Process (PEA) has been running, for some time, from other perspectives. You are invited to participate in a more interactive and dynamic educational model, where students express themselves with greater freedom and creativity. Because of this, the teacher must be very proactive and innovative.

Various studies show that there are not a few Latin American countries that see the need to implement quality didactic activities to carry out good teaching that translates into excellent learning in each of their students; one of these countries is Chile. The results that Chilean students have achieved in the mathematics subject are really worrying, since according to the information provided by the Education Quality Measurement System (SIMCE), students are at a medium level (Minte et al., 2020). Therefore, it can be understood that Chile needs to improve the level of quality of education; that is, from carrying out a systematic and methodical analysis of the level of learning achieved by their students, to the training of teachers.

On the other hand, in certain studies Ecuador showed difficulties in the mathematics subject. In the results obtained in the PISA-D 2018 tests, 70.9% of the students did not reach level two and were located at a basic level. The average performance was 337 points (Bernal et al., 2019). All this allows us to appreciate that Ecuador has not registered significant changes in favor of the Teaching-Learning Process. Students are likely to face cognitive and procedural difficulties in solving everyday problems associated with mathematics.

Mathematics at all educational levels presents a certain complexity and rigor. However, decisions can be made that favor their learning. Unfortunately, the evidence says otherwise. There are drawbacks, good links are not established between learning and the daily life of students. Even their critical and logical abilities that are not properly developed are affected. To make any decision, it is necessary to analyze the level of knowledge that children present. Knowing the reality better, various didactic activities can be prepared that, with all intention, contribute to the development of different skills.

There is a clear invitation: mathematics must be analyzed, deciphered and understood as a universal language. Taking into account that the learning and contents of this subject in the 6th grade of EGB show some applicability in the daily life of the students: "The teacher or professor will be able to guide his students to see how mathematics helps to understand daily situations and, as a consequence, to learn Mathematics" (Albertí, 2018, p. 20).

Emphasizing the 6th grade math theme,a Cartesian plane is made up of two number lines, one vertical and one horizontal. For its part, the horizontal line is called the abscissa axis or "X", and the vertical axis of the ordinates or "Y"; the point where they intersect is called the origin, respectively with a value of zero. In particular, a Cartesian plane is not only symbolized in numbers, but an infinite number of things can be incorporated.

For its part, an ordered pair is formed by two elements, with a clearly determined order (X, Y); that is, they always have an alphabetical order, there can even be an ordered pair formed by (A, B). Regarding your procedure, you must place the X axis component first and then the Y axis component, forming an ordered pair in the Cartesian plane.

Once the Cartesian plane and ordered pair have been established, it is necessary to refer to learning, because it is a process that allows us to acquire skills, knowledge, attitudes and values. In addition, taking into account that learning takes place throughout life; that is, there is always something new to learn.

On the other hand, it is necessary to take into account the standards that must sustain a quality education. These standards represent the mathematical contents and processes with which the student should be trained, providing them with something more practical than theoretical. The fact that quality mathematics is not developed with an emphasis on practice is due to the burdens that traditional education entails, in which students are receivers of information, memorizers, while the teacher leads the activity with great authority.

In addition, banking education is stimulated by understanding the contents mastered by the teacher as valuable deposits that, installed in the students' heads, they have to repeat verbatim. With these influences, a rejection by teachers of the new, of the innovative is revealed. Implying that there is no real significant progress in Ecuadorian education, learning is not memorization; learning is understanding.

If you want to train beings capable of implementing what you have learned in daily life, it is necessary to apply different methodologies; For example, discovery learning, where the teacher encourages investigative practices in students, taking into account their needs and interests. Discovery learning is based on your students creating their own knowledge and taking ownership of it, thus generating active and practical learning.

Meaningful learning is important, very encouraging and beneficial. Relates the new knowledge with the knowledge that the student already possesses; previous knowledge. For this reason, with meaningful learning, the student will be able to build their own knowledge, in the sense that they learn, investigate, and are capable of solving problems in their daily lives. However, it is essential that the teacher gets involved with his students, listening to them and conversing with them, and from there guiding them in their process.

Didactics cannot be missing from the teacher's work, neither inside nor outside the educational context. When the class works didactically, the selection and management of various media and language becomes very effective, which, with quality and efficiency, contribute to the progress and development of various skills. On the other hand, Enríquez et al. (2018) consider that the teacher is the main axis for the Teaching-Learning Process to take place, and that during their training the study of general didactics should be of great interest to achieve the construction of new experiences.

The didactic principles are beacons that illuminate the directions in the teaching task. They are a vital guide for the Teaching-Learning Process to be executed. They favor the selection of teaching aids and humanize the evaluation. According to Cano de la Cruz (2021): "The ontology of these principles focuses more on the educational fact, that is, more on Pedagogy than on Didactics, which does not detract from its significance and contribution" (p. 24).

The didactic functions of the teacher favor that he develops the class in an active way and achieves quality learning; They are vital in the organization of teaching and learning. When dealing with new content, and in reaffirmation classes, it is important that procedures prevail that guarantee a pleasant atmosphere from the positive attitude of the teacher. This influences the development of new skills that contribute to the growth of the student; In addition, in the mathematics subject it is necessary to promote logical thinking that evolves systematically in the face of problems that arise in everyday life.

Returning to Didactics, it is very favorable that the teacher knows each student. The activities are formulated based on the individual characteristics of each of them. We must understand this management as a systematic and orderly process to achieve the goals proposed in the development of the contents. For the development of the activities, according to their characteristics and depending on the contents to be treated, the children can be organized in groups or in independent work.

One of these strategies is gambling. It allows, depending on the objectives and contents, to propose activities that favor the learning processes of each one of the students. Therefore, the game helps in the construction of an adequate, integral, profitable and effective environment; that is, for the development of knowledge, to base fellowship, sociability and respect for others. The game, as a didactic strategy, strengthens various capacities in students and teachers, as mentioned by Tamayo and Restrepo (2017): "The game becomes a scenario that takes on great importance in the teaching and learning processes, since which, due to its playful component, becomes a highly motivating strategy for the participation of the subjects and in the different activities that are proposed" (p. 112).

Therefore, proposing effective activities for learning Mathematics is a constant challenge in the current educational context. They must allow the development of various skills and put logical thinking into practice. All this allows us to analyze and solve life problems, in the scenario that those involved live. "Logical-mathematical concepts constitute a fundamental and useful instrument, because through these children express their knowledge every day in each of the educational training experiences" (Lugo et al., 2019, Rev.).

For the structure of a didactic activity, some fundamental aspects must be considered. Keeping in mind the objective that students will achieve and its applicability in everyday life is very important. For this reason, it is necessary to know and analyze the knowledge that the child already knows. This will allow you to identify from which point you should start. This is how Cano de la Cruz (2021) mentions it: "You should always start from what your previous knowledge is, to detect what you do not know and base learning on what you know, and start from the idea that the student will understand much better that of which he has a prior idea" (p. 156).

Previous knowledge is enriched with new knowledge, but it is important to guide students towards what, how and why they are going to learn about what is proposed. In this way, the new vision of their learning evolves. Even the role of the teacher consists of knowing the students, knowing what they know, who they are, what they need and corresponding to their Teaching-Learning Process. Therefore, preferably the activities should be interactive, dynamic and a proposal to the needs and interests of the students. Finally, the teacher must verify if the objective proposed for the activity was achieved.

Analyzing the level of knowledge that EGB 6th grade students have ^willallow the design of relevant didactic activities in favor of their learning. Motivation, interpersonal relationships and daily life should not be lost sight of. The didactic game can favor, to a great extent, taking into account that play is as important for children as work is for adults.

This research work was developed from a quantitative approach. The quantitative approach, from the vision of Gómez (2006): "Uses data collection and analysis to answer research questions and test previously established hypotheses, and relies on numerical measurement, counting, and the use of statistics "(p. 70). On the other hand, it was developed under a non-experimental design. Gómez (2006) mentions that: "Phenomena must be observed as they occur in their natural context, and then analyzed" (p. 60). That is to say, it was carried out without manipulation of variables.

In addition, the study has a descriptive nature. Gómez (2016) establishes that: "The information necessary for the analysis is made up of the frequency distribution, measures of central tendency and measures of variability" (p. 140); Summarizing, for this research the application of statistics, numerical measurement and percentage analysis, from a diagnosis that allows describing the state of knowledge of the group.

The population was considered 15 students between boys and girls organized in the only group of 6 ^thgrade of EGB of the Educational Unit "Julio Moreno Espinosa". According to Hernández et at. (2010) defines as "Population or universe the set of all cases that match certain specifications" (p. 174). The sample was constituted by 100% of the population. It was selected in a non-probabilistic way for the convenience of the study. It is worth mentioning that a sample is understood as a subset of the population to which the investigation is going to focus.

The dependent variable, considered for this research, is learning about the location of ordered pairs in the Cartesian plane with natural numbers. According to Espinoza (2018), he affirms that: "They constitute the effects or consequences that give rise to the results of the investigation" (Rev.). From its analysis, four indicators and three levels of knowledge were established: high, medium and low.

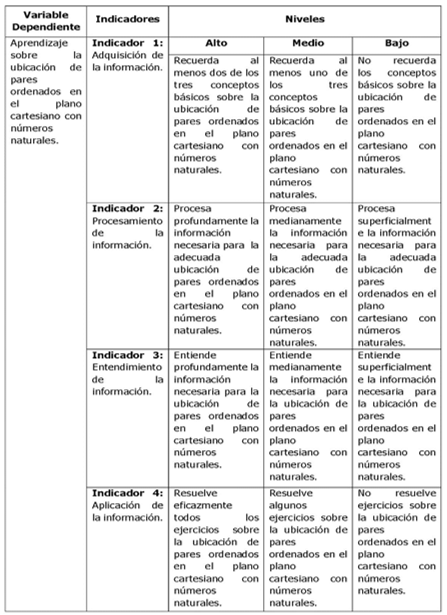
On the other hand, descriptive statistics were applied. "Descriptive statistics is the branch of statistics that formulates recommendations on how to summarize, in a clear and simple way, the data of an investigation in charts, tables, figures or graphs" (Rendón et al., 2016, Rev.). In addition, the statistical package SPSS was used. For Rivadeneira et. al (2020) this tool is used in almost all branches of science, emphasizing its usefulness in data quantification, as well as its easy understanding.

To describe the level of knowledge presented by 6th grade EGB students. Garces et al. (2018) mention that: "Knowledge creates bridges that go through the assimilation process so that new information becomes a potentially significant instrument, to transcend in the sense of learning to learn" (p. 5).

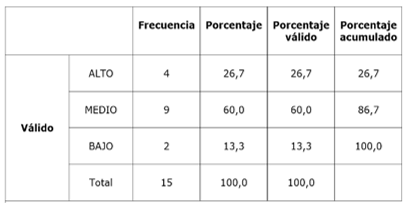
Regarding this indicator, it is evident that 26.7% reach a high level of knowledge. It means that four students remember at least two of the three basic concepts evaluated. However, 13.3%, two students, manifest themselves at a low level. It means that they do not remember any concept. This can negatively influence the assimilation of other contents during the mathematics subject in the current course and in subsequent levels. Finally, 60%, the highest percentage, are at a medium level of knowledge. This declares that they do remember the basic information necessary to solve exercises related to the topic in question.

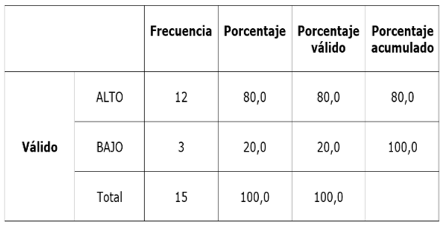
As can be seen, in this case, 80% of the students achieve a high level of knowledge. It is significant and encouraging that 12 students concretely process the information necessary to solve problems associated with these issues that are of vital importance, at least, for school life. However, 20%, three students, are located at a low level. It means that they do not assimilate or superficially assimilate the information to correctly locate the ordered pairs in the Cartesian plane with natural numbers.

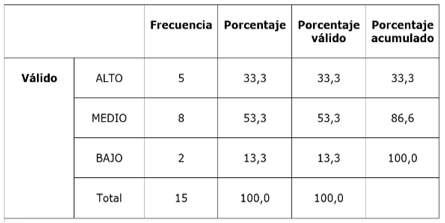
In the analysis on the understanding of the information there are five students, 33.3%, who show a high level of knowledge. In other words, they manage to understand very well the information necessary for the correct resolution of exercises on the topics of interest in favor of their daily life. On the contrary, 13.3% are shown at a low level. In other words, they have problems understanding information, presenting problems with learning during this course. On the other hand, with the highest percentage of students, 53.3% of those evaluated are located at the intermediate level. It could be said that eight students do understand, but little, about the location of ordered pairs in the Cartesian plane with natural numbers.

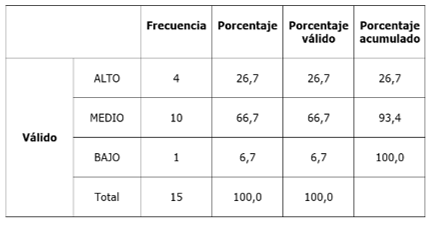
When applying the information, only four students, 26.7%, manage to do it very effectively and are located at a high level. They managed to adequately solve the exercises on the location of ordered pairs in the Cartesian plane with natural numbers, so they have important skills to manage and solve problems of daily life. Unfortunately, one student, representing 6.7%, shows a low level of knowledge. That is to say, they have few abilities to solve the proposed exercises. If these issues are not systematically worked on in class, these difficulties may be dragged to higher levels. At the medium level, 66.7% can be seen, with the highest percentage. A total of 10 students, the majority, are the ones who can solve only a few exercises on these math topics related to everyday life.

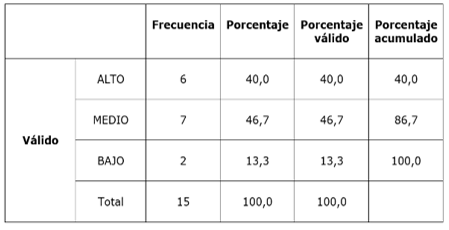
From a more holistic view, it can be seen that six students, 40.0%, are at a high level of knowledge. This reflects that they have theoretical mastery of the subject and can solve various problems of daily life related to these contents. With whom you have to work the most is with 13.3%, two students, who are located at a low level. Such students may have difficulty learning at higher levels, which require these foundations as prerequisites. 46.7% of students are at a medium level and constitute the majority. They achieve a basic level on the location of ordered pairs in the Cartesian plane with natural numbers. In order for students who are in the low and medium levels to advance to the high level, it is necessary that the proposal of activities consider the shortcomings that most affect learning on the topics covered. Without negativity blinding the eyes of the educator, it worries that these students, far from evolving, regress.

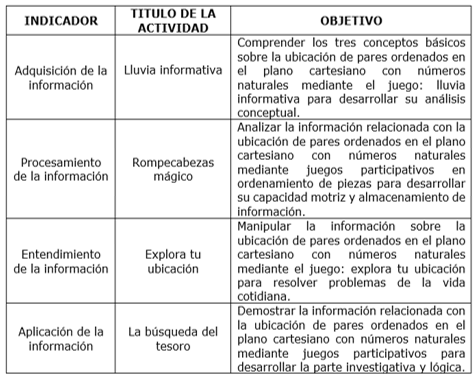
It is necessary to propose ten activities that favor the learning of 6th grade EGB students, in relation to each of the indicators. Through the activities it is possible to develop the subject in a more active, dynamic way and relationships are established with daily life. Each activity is linked to educational games. In the following table there is a sample of four activities that respond to each indicator (acquisition, processing, understanding and application), respectively. Through the QR code or link shown, it will be possible to visualize the rest of the activities more explicitly.

The state of knowledge was determined and it was possible to show that the students are at a medium level of knowledge. Garces et al. (2018) consider that the level can be determined based on the information obtained and received in a transcendental way and during a specific period. To a lesser extent, there are difficulties in the acquisition of information to master the fundamental concepts. The most alarming thing occurred at the time of solving the exercises, considering that this is the application phase.

In this way, 10 didactic activities on the location of ordered pairs in the Cartesian plane with natural numbers are proposed. The activities are necessary and advantageous when developing their learning and generating new experiences; for this, each of the indicators was taken into account. In addition, the game was considered for how favorable it can be for learning about these topics. According to Tamayo and Restrepo (2017), the game is of great importance in the Teaching-Learning Process, thus becoming a motivating strategy for students, which leads them to achieve greater participation.

An investigation carried out by Cuesta in Colombia reaffirms that the game is an important factor in the development of academic content and interaction among their peers, it also helps to achieve significant learning in students.

This proposal of activities has a formative character: allow the proper development of logical and critical thinking, emphasizing situations closely linked to the daily life of students. According to Albertí (2018), he mentions that: "Two fundamental aspects relate mathematics to life: its usefulness and it helps understanding" (p. 18). In other words, it is important to develop the appropriate processes to understand mathematics as a valuable and important area of knowledge in their day to day.

Furthermore, in the words of Lugo et al. (2019), logical-mathematical development is useful and basic; Through it, students experience and acquire knowledge on a daily basis. Another of the goals of the proposal is to contribute to the acquisition of a broader vision of how to learn and how to teach mathematics in a dynamic way. Always reflecting on the objectives proposed by the curriculum and the analysis of the contents necessary to overcome them.

Therefore, students show difficulties in the acquisition of information and resolution of exercises, and problems may arise for learning about very important topics that are supported by the location of ordered pairs in the Cartesian plane with natural numbers . In this way, the proposed didactic activities are the result of a deep reflection on the shortcomings and potential of the students, always considering the topics of interest for this research and the importance of training that responds to the current needs of society.

Bernal Reino, J. C., Calle Palomeque, C. E., Guachún Lucero, F. P., & Mora Naranjo, B. M. (2019). Investigación en Educación Matemática, en Ecuador y la Región: Caso Universidad de Cuenca. En La Investigación Educativa en un Mundo en Constante Transformación (p. 35). PESAD Plataforma para un Desarrollo Académico Sustentable en Ecuador. http://dspace.ucuenca.edu.ec/bitstream/123456789/34211/1/documento.pdf

Cano de la Cruz, Y. (2021). Didáctica General: Una aproximación a su estudio. Quito, Centro de Publicaciones de la Pontificia Universidad Católica del Ecuador. Estudios sobre Educación, 41, 253-254. https://doi.org/10.15581/004.41.41069

Enríquez Clavero, J. O., González Hernández, G., & Cobas Vilches, M. E. (2018). ¿Qué didáctica desarrollar, la general y/o las particulares? Reflexiones desde su epistemología. Edumecentro, 10(3), 140-157.

Espinoza Freire, E. E. (2018). Las variables y su operacionalización en la investigación educativa. Revista Conrado, 14(65), 65.

Espinoza Freire, E., Tinoco Izquierdo, W. E., & Sánchez Barreto, X. del R. (2017). Características del docente del siglo XXI (original). Olimpia: Publicación científica de la facultad de cultura física de la Universidad de Granma, 14(43), 39-53.

Garcés Cobos, L. F. G., Montaluisa Vivas, Á., & Salas Jaramillo, E. (2018). El aprendizaje significativo y su relación con los estilos de aprendizaje. Revista Anales, 1(376), 376. https://doi.org/10.29166/anales.v1i376.1871

Gómez, M. M. (2006). Introducción a la metodología de la investigación científica (1era ed.). Brujas.

Lugo Bustillos, J. K., Vilchez Hurtado, O., & Romero Álvarez, L. J. (2019). Didáctica y desarrollo del pensamiento lógico matemático. Un abordaje hermenéutico desde el escenario de la educación inicial. Revista Logos Ciencia & Tecnología, 11(3), 18-29. https://doi.org/10.22335/rlct.vlli3.991

Minte, A., Sepúlveda, A., Díaz, D. y Payahuala, H. (2020). Aprender matemática: dificultades desde la perspectiva de los estudiantes de Educación Básica y Media. Espacios, 41(9),1-7. https://www.revistaespacios.com/a20v41n09/a20v41n09p30.pdf

Rendón-Macías, M.-E., Villasís-Keever, M., & Miranda-Novales, M. (2016). Estadística descriptiva. Revista Alergia México, 63, 397. https://doi.org/10.29262/ram.v63i4.230

Tamayo Giraldo, A., & Restrepo Soto, J. A. (2017). El juego como mediación pedagógica en la comunidad de una institución de protección, una experiencia llena de sentidos. Revista Latinoamericana de Estudios Educativos 13(1),105-128. https://www.redalyc.org/articulo.oa?id=134152136006