
Mendive. Journal on Education, January-March 2023; 21(1): e3007 
Translated from the original in Spanish
Original article
Didactic strategy to develop the ability to calculate definite integrals from creative learning
Estrategia didáctica para desarrollar la habilidad calcular integrales definidas desde un aprendizaje creativo
Estratégia didática para desenvolver a capacidade de calcular integrais definidas a partir do aprendizado criativo
Wilfredro Sanchez Companioni1![]() https://orcid.org/0000-0002-3033-9430
https://orcid.org/0000-0002-3033-9430
Andel Pérez González1
![]() https://orcid.org/0000-0003-4435-4030
https://orcid.org/0000-0003-4435-4030
Juana María Remedios
González1![]() https://orcid.org/0000-0001-7030-5326
https://orcid.org/0000-0001-7030-5326
1University of Sancti Spíritus José Martí Pérez. Cuba ![]() wilfredosc@uniss.edu.cu, apgonzalez@uniss.edu.cu, jremedios@uniss.edu.cu
wilfredosc@uniss.edu.cu, apgonzalez@uniss.edu.cu, jremedios@uniss.edu.cu
| Sánchez Companioni , W., Pérez González, A., & Remedios González, J. (2023). Didactic strategy to develop the ability to calculate definite integrals from creative learning. Mendive. Revista de educación, 21(1), e3007. https://mendive.upr.edu.cu/index.php/MendiveUPR/article/view/3007 |
Received: March 31, 2022.
Accepted: October 27, 2022.
ABSTRACT
The development of skills in the training of university professionals is a very topical topic; above all, if one takes into account that they express the know-how of the students and their relationship with the world of work for which they are being prepared. Hence, the importance of developing the ability to calculate definite integrals in the students of the Bachelor of Accounting and Finance; since this facilitates the solution of various situations typical of the profession. That is why, this article had the objective of socializing a didactic strategy aimed at the development of the ability to calculate definite integrals, from a creative Teaching-Learning Process of the Higher Mathematics I subject. For its design, a quantitative methodology was used that required the use of theoretical methods such as the historical-logical, the analytical-synthetic and the inductive-deductive, which made possible the theoretical foundation of the didactic strategy; as well as the empirical ones: review of the product of the activity and the observation, to know the level of development of the ability in the students who participated in the investigation. The main result was constituted, precisely, by the didactic strategy and the methodological suggestions for its implementation. Its application in practice evidenced favorable transformations in the level of development of the skill under analysis; thus, reaffirming its feasibility and, above all, the relevance of creative learning.
Keywords: creativity; didactic strategy; ability; calculate definite integrals; creative learning and mathematics.
RESUMEN
El desarrollo de habilidades en la formación de los profesionales universitarios constituye una temática de gran actualidad; sobre todo, si se tiene en cuenta que en ellas se expresa el saber hacer de los estudiantes y su relación con el mundo laboral para el que se preparan. De ahí, la importancia de desarrollar la habilidad calcular integrales definidas en los estudiantes de la carrera Licenciatura en Contabilidad y Finanzas; ya que esta facilita la solución de diversas situaciones propias de la profesión. Es por ello que, este artículo tuvo como objetivo socializar una estrategia didáctica dirigida al desarrollo de la habilidad calcular integrales definidas, desde un Proceso de Enseñanza-Aprendizaje creativo de la asignatura Matemática Superior I. Para su diseño se utilizó una metodología cuantitativa que exigió el empleo de métodos teóricos como el histórico-lógico, el analítico-sintético y el inductivo-deductivo, los que hicieron posible la fundamentación teórica de la estrategia didáctica; así como los empíricos: revisión del producto de la actividad y la observación, para conocer el nivel de desarrollo de la habilidad en los estudiantes que participaron en la investigación. El principal resultado lo constituyó, precisamente, la estrategia didáctica y las sugerencias metodológicas para su implementación. Su aplicación en la práctica evidenció transformaciones favorables en el nivel de desarrollo de la habilidad objeto de análisis; reafirmándose así su factibilidad y, sobre todo, la pertinencia del aprendizaje creativo.
Palabras clave: creatividad; estrategia didáctica; habilidad; calcular integrales definidas; aprendizaje creativo y matemática.
RESUMO
O desenvolvimento de competências na formação de profissionais universitários é um tema de grande relevância; sobretudo, se tivermos em conta que expressam o saber-fazer dos alunos e a sua relação com o mundo do trabalho para o qual estão a preparar-se. Daí a importância de desenvolver a capacidade de calcular integrais definidas nos alunos da carreira de Bacharel em Contabilidade e Finanças; já que isso facilita a solução de diversas situações da profissão. É por isso que este artigo teve como objetivo socializar uma estratégia didática que visa desenvolver a capacidade de calcular integrais definidas, a partir de um processo criativo de Ensino-Aprendizagem da disciplina de Matemática Superior I. Para seu desenho, foi utilizada uma metodologia quantitativa que exigiu o uso de métodos como o histórico-lógico, o analítico-sintético e o indutivo-dedutivo, que possibilitaram a fundamentação teórica da estratégia didática; bem como os empíricos: revisão do produto da atividade e observação, para conhecer o nível de desenvolvimento de habilidades nos alunos que participaram da pesquisa. O principal resultado foi justamente a estratégia didática e as sugestões metodológicas para sua implementação. Sua aplicação na prática evidenciou transformações favoráveis no nível de desenvolvimento da habilidade em análise; reafirmando assim a sua viabilidade e, sobretudo, a relevância da aprendizagem criativa.
Palavras-chave: criatividade; estratégia didática; habilidade; calcular integrais definidas; aprendizagem criativa e matemática.
INTRODUCTION
The economy, culture and social policies at the international and national level are currently characterized by successive transformations that respond to the rapid progress of science, technique and technology; as well as the demands of society. In this sense, university education must ensure the training of competent professionals, capable of assuming the challenges of the present and the future.
In this regard, the Ministry of Higher Education in Cuba (MES), aware of its responsibility in the constant improvement of the Cuban social project, has as a priority the continuous improvement of the training process of university professionals. On this matter, it is specified that the university must be distinguished by the formation of values and by the assurance of the quality of its substantive processes, in order to achieve a graduate who possesses personal qualities, culture and professional skills that allow them to perform with social responsibility.
Faced with this requirement, the Teaching-Learning Process (PEA) in universities must promote the training and development of the necessary skills to fulfill the professional functions of each career. Only in this way, its graduates will achieve a better insertion in the social and productive dynamics of the profession. That is why the Mathematics Teaching-Learning Process is analyzed, as:
A process in which both teaching and learning are subsystems that guarantee the active, creative, reflective, significant and motivated appropriation of the content as part of the comprehensive general culture, taking into account current developments, with the purpose of continuously expanding the boundaries of the zone of potential proximal development. This implies affective communication and the development of intentional activities, whose didactic actions generate learning strategies that allow learning to learn Mathematics, as an expression of the constant development of a comprehensive and self-determined personality of the student (Ballester Pedroso, García La Rosa, Almeida Carazo, Álvarez Pérez, Rodríguez Ortiz, González Noguera, Villegas Jiménez, Fonseca González, and Puig Reyes, 2018, p. 13).
From this perspective, preparing students to apply mathematical knowledge to solve professional accounting and finance problems is identified as a complex task. Hence, a fundamental role is assigned to the learning of the contents that are related to the calculation of definite integrals, for what they contribute to the understanding and solution of problems of the Degree in Accounting and Finance (Sánchez Companioni, Pérez González and Remedios González, 2022) and, in particular, to the training and development of the corresponding skills. Hence, the definition of Ferrer Vicente and Rebollar Morote (1995) is assumed, where they refer that:
A mathematical ability is the construction, by the student, of the way of acting inherent to a certain mathematical activity, which allows him to search for or use concepts, properties, relationships, mathematical procedures, use work strategies, perform reasoning, judgments that are necessary for solve mathematical problems (p. 5).
By delving into the Teaching-Learning Process of the calculation of definite integrals, Suárez Rincón (2018) underlines the relevance of using novel resources that facilitate the understanding of the concepts and the development of specific mathematical skills of this topic; Consequently, the ability to calculate definite integrals is considered as: the operation by which the value of the determined area is obtained between the curve that determines the function and a segment of the coordinate axis determined by an interval [a,b], in the which said curve is integrable. Said value results from the calculation of the primitive corresponding to the analytical expression of the curve and the application of the fundamental formula of the integral calculation.
Consequently, a general procedure is used to work on the formation and development of
the ability to calculate indefinite integrals that summarizes the actions that students must master.
It implies: the analysis of the integrand to decide if the integral is immediate or not (if its
primitive is calculated using only the properties and rules of integration or if an integration method is
also needed); if the integral is immediate, the properties of the indefinite integral and the
integration rules to be used are identified, and if it is immediate, the integration method to be used
is selected; the primitive of the function f(x) is calculated: F(x); the fundamental formula of
integral calculus is applied ![]() ; the numerical values of F (b) = B and F (a) = A are calculated; A,B
; the numerical values of F (b) = B and F (a) = A are calculated; A,B![]() and the value of is calculated
and the value of is calculated![]()
On the other hand, Fonseca Castro and Alfaro Carvajal (2018) state the usefulness of using modeling, problem solving and technological tools as learning strategies. Likewise, for Villena Muñoz and Rivas Maldonado (2019) it is pertinent to master the calculation procedures and apply them to the solution of problems. While Granera Rugama (2019) points out that learning the contents of the calculus of definite integrals means understanding the meaning of the concepts, mastering the procedures and developing calculus skills; Regarding this, it prioritizes the use of teaching methods that promote the development of advanced mathematical thinking and the use of technology.
Similarly, Martínez Castellini (2020) believes that, since there is no procedure to calculate integrals, teaching tasks acquire the connotation of a problem; which justifies the use of methods that promote reflection, productive activity and the development of creative thinking of students and, in this sense, Rojas Taño and Rodríguez Sosa (2021) highlight the value of contextualizing the contents to the problems of each race.
These ideas are related or complemented by being consistent with creative learning; seen this as:
A way of learning that differs from the common ways of learning in the school environment, and is characterized by the type of production that the apprentice makes and by the subjective processes involved in it (...) This learning has different forms of expression and in In it, a set of subjective resources participate and is expressed in the configuration of at least three processes: the personalization of computerization, the confrontation with what is given and the production of own and new ideas ( Mitjáns Martínez, 2013, p. 317).
In spite of this, although in general the consulted works address aspects of interest for the Teaching-Learning Process of definite integrals, it was not possible to find specific studies that focused their attention on the development of the ability to calculate definite integrals. Consequently, this article reflects on the following question: what way can be used to contribute to the development of the ability to calculate definite integrals from the PEA of the Higher Mathematics I subject?
Meanwhile, in response to the previous question, the authors set out as an objective to socialize a didactic strategy that contributes to the development of the ability to calculate definite integrals, from a creative Teaching-Learning Process of the Higher Mathematics I subject.
Its importance lies in the fact that it offers mathematics teachers a different way to promote the development of the ability to calculate definite integrals; in this case, from the particularities of creative learning. Its scope is given by what it can mean for the development of the referred ability in the students of the Accounting and Finance Degree and in other university careers; as well as the possibility of transferring what is related to creative learning to other mathematical contents.
MATERIALS AND METHODS
To answer the question posed by the authors, it was necessary to use a quantitative methodology that facilitated the use of theoretical and empirical methods.
Of the theoretical, the historical-logical, the analytical-synthetic and the inductive-deductive were used; those that allowed to determine the theoretical positions around the PEA of Mathematics and, in particular, of the definite integrals and creative learning. Likewise, they facilitated the study of mathematical skills and their development.
On the other hand, it was necessary to resort to the analysis of the product of the activity and to observation as empirical methods; those that made it possible to deepen the study of the level of development of the mathematical ability to calculate definite integrals in the students participating in the research. The performance of the students was observed during the solution of different types of tasks that required the calculation of definite integrals used in practical classes. With the same intention, the notes that described the solution of the tasks resolved in the subject notebooks, the written evaluations and in other class works were reviewed.
Hence, the unit of analysis will be determined as the students of the Accounting and Finance Degree of the "José Martí Pérez" University of Sancti Spíritus; The population was made up of 34 students of the aforementioned career and the nine first-year students were part of the sample with which we worked during the application of the didactic strategy, since this was the moment where the content being studied was taught.
For the processing of the information resulting from the diagnosis and the implementation of the didactic strategy, statistical-mathematical methods were used; in particular, the descriptive statistics and, from it, the measures of central tendency and the graphical representation for its better interpretation. On the other hand, methodological triangulation was used to achieve greater objectivity and credibility of the analysis of the information obtained from the application of the empirical methods described above.
RESULTS
This section begins with the results of the diagnosis of the level of development of the ability to calculate definite integrals in the students selected from the population. These allowed us to assess the design of a didactic strategy as a possible solution to the problem posed.
By assuming as an object to evaluate the development of the ability to calculate definite integrals, cognitive, procedural and attitudinal indicators were specified that derive from the theoretical positions assumed in the introduction of the article. The cognitive ones reflect the essential knowledge to achieve the development of the corresponding ability and its necessary understanding by the students, these were: mastery of the knowledge necessary for the calculation of indefinite (1) and definite integrals respectively (2); as well as professional knowledge related to definite integrals (3). The particular procedures include, in each of the two, the actions and operations that the students had to know how to do to calculate definite integrals, they were: the application of the procedure associated with the calculation of indefinite integrals (4); the application of the procedure associated with the calculation of definite integrals (5) and the application of the calculation of definite integrals to the solution of professional problems (6).
Meanwhile, the attitudes evaluated were: the implication (7), the satisfaction (8) and the disposition (9) of the students during the solution of tasks of calculation of definite integrals.
For the measurement, the empirical methods specified in the introduction and an ordinal scale that considered the categories of Very Adequate (MA), Quite Adequate (BA), Adequate (A), Little Adequate (PA) and Inadequate (I) were used.
Graph 1 shows the results, after observing the performance of the students during the development of the practical classes and reviewing the products made by them in notebooks and written evaluations of calculus of definite integrals.
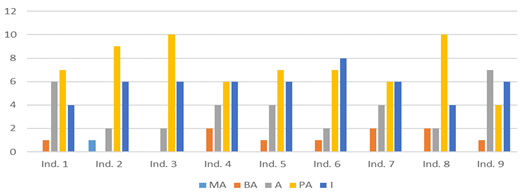
Graph 1- Results of the evaluated indicators (own elaboration)
The qualitative analysis of the results showed that the students:
They knew the definition of indefinite integral, but without understanding its meaning, and they identified the properties and rules of integration of elementary functions.
They recognized the methods of integration, but did not understand its steps, nor did they understand the necessary and sufficient conditions of the Fundamental Theorem and Mean Value.
Generally, they did not prioritize the analysis of the professional in the application exercises and only concentrated on what was related to mathematics.
They knew the actions to calculate indefinite integrals, but they did not perform an analysis of the integrand. Sometimes they chose the method well, but they did not control their actions.
They frequently made mistakes when applying the integration methods, when determining the primitive, and when using the Fundamental Theorem of Integral Calculus and Mean Value.
They hardly ever succeeded in modeling the problematic situations related to the profession and in no case did they delve into their professional meaning.
They were not always active when carrying out the tasks, they did not consider them important for their profession and they did not generate ideas and solutions of their own.
They were dissatisfied, as they frequently made mistakes and also did not understand the content and its practical application to the profession.
The described results evidenced a contradiction between the actual state of development of the ability to calculate definite integrals and the required one. Hence, the need to design a didactic strategy that would allow the transformation of said reality, which is described below.
The didactic strategy that is socialized, starts from considering the theoretical positions of Rodríguez del Castillo and Rodríguez Palacios (2011) and the experiences that guide the fulfillment of an objective and allow the organization, planning, execution and evaluation of the PEA. Hence, the didactic strategy is assumed as the projection of a system of actions in the short, medium and long terms, which allows the transformation of the Teaching-Learning Process in a subject, level or institution based on its components and which allows the achievement of the proposed objectives in a specific time (Rodríguez del Castillo and Rodríguez Palacios, 2011, p. 39).
Consequently, its criteria are followed in relation to the structure of the strategy; This specifies its theoretical foundations, its general objective and its stages containing specific objectives, actions and suggestions for its realization, as well as the guidelines that guide its implementation and evaluation.
The fundamentals of the didactic strategy were organized in three directions: the Teaching-Learning Process of Mathematics, the development of the mathematical ability to calculate definite integrals and creative learning.
In the first direction, the developer approach of the Mathematics Teaching-Learning Process is signified and activation-regulation, significance and motivation are considered as its dimensions (Ballester Pedroso, García La Rosa, Almeida Carazo, Álvarez Pérez, Rodríguez Ortiz, González Noguera, Villegas Jiménez, Fonseca González, and Puig Reyes, 2018) and, in relation to them, it is stated that for the development of the skill under analysis it is necessary for students to master the concepts, propositions, procedures, techniques , work strategies and development of feelings, attitudes and values; that they identify the different types of learning tasks, the strategies for their solution and the control mechanisms for the correction of the tasks and, in particular, that they appropriate the general procedure worked on in the introduction; as well as, establish relationships between the new knowledge with the previous ones and with those of other subjects and reconstruct their ways of thinking and acting in different contexts of professional learning.
A significant value is also attached to the requirement that makes explicit what is related to the development of creativity from the methodological approach of the PEA of Mathematics. This specifies the need to "promote development towards higher levels of performance, through the performance of interdisciplinary tasks and the progressive transition from dependence to independence and creativity" (Álvarez Pérez, Almeida Carazo and Villegas Jiménez, 2014, p.1).
Emphasis is placed on the need for students to be motivated and active while carrying out various tasks, on the relevance of using technologies for heuristic purposes so that they can acquire knowledge and rationalize mental work, and on the importance of interacting, reflecting and cooperate with each other when solving the learning tasks (Álvarez Pérez, Almeida Carazo and Villegas Jiménez, 2014) related to the calculation of integrals.
On the other hand, the theoretical elements of interest for the PEA of the defined integrals are specified, from the relationships between the components of the PEA.
From the objective, it is necessary to point out the need for the PEA of definite integrals to promote the development of logical thinking of students and their integral formation (Granera Rugama, 2019). Meanwhile, the essential knowledge and skills that this content provides for their professional development should be highlighted (Fonseca Castro and Alfaro Carvajal, 2018) and, above all, the procedures to be used in each case of the calculation of integrals and their links with the disciplines. of the profession.
Meanwhile, for the Teaching-Learning Process of these contents, methods must be used that promote the development of mathematical thinking (Granera Rugama, 2019) and that favor the formulation of conjectures, inductive processes and argumentation (Fonseca Castro and Alfaro Carvajal, 2018) of the actions and operations necessary for the development of the skill.
Likewise, it is necessary to select means that allow problematic situations to be modeled, promote the transition towards cognitive independence of students and stimulate the integration between teacher-student-knowledge-technology and with the context (Villena Muñoz and Rivas Maldonado, 2019), standing out as the use of ICT is essential.
Particularly, the types of tasks are emphasized as part of the forms of organization; which should require the approach and solution of contextualized problems, where mathematical modeling is necessary and the use of strategies that stimulate the active participation of students for their solution from meaningful learning (Rojas Taño and Rodríguez Sosa, 2021).
According to the above, the requirements are specified to achieve creative learning of the calculation of definite integrals in students of the Accounting and Finance career:
Set learning objectives for the study of mathematical content and individualized goals for their fulfillment.
Attribute meaning to mathematical knowledge and skills (concepts, propositions, procedures, mathematical work strategies, skills).
Establish relationships between mathematical knowledge and skills with background content and other subjects.
Identify, formulate and solve problems of mathematics, other sciences or practical life where the application of mathematical content is necessary.
Act with motivation, cognitive independence and originality while searching for various solutions to tasks that require the application of mathematical content in different contexts.
Use learning methods that promote their independent, original and motivated participation during the application of mathematical knowledge and skills in different contexts.
Use procedures that promote the development of ways of working and mathematical thinking during the application of mathematical knowledge and skills in different contexts.
Use or develop learning media that facilitate the application of mathematical knowledge and skills in different contexts.
Present, argue and evaluate their ways of solving the tasks and those of their classmates.
Establish relationships with their classmates and with the teacher, in a pleasant and collaborative climate (Sánchez Companioni, Pérez González and Remedios González, 2022, 325-326).
The second direction takes up the elements on which the work with the mathematical skill that is intended to be developed with the didactic strategy is based and pays attention to the methodological conditions to follow for the development of a skill: work, first with simple executions and then more complex, gradually graduate the periodicity of actions and operations, apply the skill in various contexts, require continuous improvement of the actions and operations that determine the skill, and foster student motivation for the conscious performance of different types of tasks in which the ability is used.
Finally, the third direction has to do with creative learning. In this regard, creativity is considered its fundamental form of expression and this should promote the production of meanings and subjective configurations (Mitjáns Martínez, 2013); Hence, the way of conceiving and carrying out teaching is essential. The author herself insists on the need to prioritize the production of novel ideas, as well as offering the student the possibility of going beyond what is established and getting involved in the production of their own resources to learn to carry out the actions and operations that correspond to the calculation of definite integrals.
In addition, it is taken into account that learning creatively is expressing yourself differently, since each student has their own thinking about things in the school environment and that creative learning stimulates the solution to a problem based on experience and highlights the idea of there may be multiple solutions.
Meanwhile, the following stand out as ways that stimulate it: the construction of knowledge, collaboration, communication, the use of information and communication technologies, self-assessment, the innovative solution of real problems and questioning (Rodríguez Saltos, Vallejo Loor, Yenchong Meza and Ponce Solórzano, 2020).
In addition, their subjective processes are analyzed from the positions of Mitjáns Martínez (2013) herself, when she explains that the personalization of information occurs when it acquires meaning for students; that is, when the assimilated information is transformed by operating with it in different conditions and contexts. Also, when the confrontation with what is given implies the questioning and problematization of the information; the non-acceptance of what is given as the only alternative and contradictions that stimulate the production and generation of new ideas are identified or raised. Meanwhile, the production and generation of their own ideas about what is studied makes it necessary for students to identify new options and formulate hypotheses about the object being studied.
Being consistent with the above, the designed didactic strategy is distinguished by promoting creative learning, which is expressed in: the personalization of information, the confrontation with what is given, the problematization of information and the production and generation of own ideas. It is conceived based on the fact that the PEA meets the following requirements: use mathematical and professional problems for the acquisition and fixation of knowledge; use Information and Communication Technologies (ICT) as a means to obtain information and generate learning; stimulate interest in the production of knowledge; promote imagination, curiosity, problematization and the generation of own ideas and encourage active participation while carrying out tasks.
Then, its general objective is to contribute to the development of the ability to calculate definite integrals in the students of the Degree in Accounting and Finance; hence actions for teachers and students are included. For its design, three interrelated stages were determined: diagnosis, planning and execution.
Diagnostic stage
Objective: to evaluate the mastery of the antecedent contents necessary for the development of the ability to calculate definite integrals and the conditions for the achievement of creative learning in the students of the career.
Actions to be carried out: determination of the antecedent contents to be evaluated and of the manifestations that show creative learning, elaboration of the instruments, application of the instruments and triangulated analysis of their results, determination of the potentialities and difficulties to be considered for the development of the skill calculate definite integrals and projection of corrective actions to solve difficulties.
General suggestions for carrying out the actions
The determination of the antecedent contents requires reviewing the program of the discipline and subject, as well as other texts and teaching materials. In the case of the manifestations of creative learning, the theoretical positions assumed must be analyzed. It is suggested to use instruments where it is possible to interact with the students; that is to say: the observation, the review of the product of the activity and the interview. Prior to its application, it is necessary to ensure the commitment of the students so that the information obtained is more truthful and reliable. Their results are analyzed independently and triangulated to identify regularities; the problems must be analyzed with the students, so that they become involved in the corrective actions.
Planning stage
Objective: to design, in the medium and short term, the process of formation and
development of the ability to calculate definite integrals.
Actions to be carried out: formulation of the objectives to be met, selection of the contents
to be developed, determination of the methods, selection or design of teaching aids,
identification of the types of tasks, design of evaluation pathways and selection of organizational forms; in
all cases, those that promote creative learning should be prioritized.
General suggestions for carrying out the
actions
The objectives are derived from those proposed by the discipline and subject, managing to
make explicit their connection with professional problems. An example could be: solving definite
integral calculation problems, which allow the analysis of situations typical of Accounting and
Finance, through the application of different integration methods.
When determining the contents, the knowledge, skills and professional attitudes to be
acquired by the students must be specified. Also, the ways of working and thinking and the most
feasible strategies to achieve creative learning are identified; Examples of the latter are: the variation
of conditions and the search for relationships.
The selection of the methods must prioritize those that stimulate the active and
independent participation of the students; that is to say: the problematic exposure, the partial or
heuristic search or the investigative one. They can integrate problem-based or project-based learning
and heuristic procedures, given their potential to obtain original solutions. When selecting the
media, the texts are prioritized: Calculus with early transcendentals
and Higher Mathematics I and II; as well as
Geogebra and Derive.
In this sense, the study guides must include varied tasks that imply the use of strategies
that promote the achievement of creative learning. The types of tasks to be used are:
identification and formulation of accounting problems, calculation of definite integrals immediately,
calculation of definite integrals applying the different methods of integration and resolution of
problems whose solution requires the calculation of definite integrals.
When designing them, it is necessary to take into account their objective, that they
integrate mathematical and professional knowledge and skills and that they encourage ways of acting
that are typical of creative learning. Likewise, they must offer the possibility of unlimited depth in
the study of the contents and their professional applications; prompt reflection; stimulate
the possibilities of choice, decision-making and self-assessment on the part of students; as well
as the gradual increase in its complexity and degree of difficulty.
The ways and forms of evaluation must require mastery of knowledge and its application;
promote the elaboration and verification of hypotheses, the problematization, the questioning during
the solution of the exercises and problems. It is also necessary to prioritize the carrying out
of investigative work that stimulates the production of knowledge in close connection with
the profile of the career professional.
The forms of organization to be used must promote the achievement of creative learning; that
is, encourage students to search, reflect, develop their own theories and, above all, do it
autonomously. It is suggested to develop different types of classes, tutorials, study practices and consultations.
Execution stage
Objective: to teach the classes that correspond to the process of formation and development of the ability to calculate definite integrals.
Actions to be carried out by teachers: orientation of the tasks to be carried out in class or other forms of organization, development of systematic exchanges with students, control of the solution process and the result of the tasks, evaluation of the fulfillment of the objective by the students and creation of a favorable climate during learning.
General actions to be carried out by the students: problematization of the contents related to the calculation of integrals, formulation of questions associated with the content, modeling of problems of the profession, approach and verification of hypotheses associated with the solution of exercises and problems of calculation of integrals defined, exposition and argumentation of solution paths and the results obtained, as well as critical and self-critical assessment of the solution paths and the results.
Specific actions to be carried out by the students: identification and formulation of problems or professional situations where definite integrals make sense, preparation and application of procedures for calculating definite integrals, preparation and application of a particular heuristic program for solving calculation problems of definite integrals, elaboration of a content material of professional situations that are solved by means of the calculation of definite integrals.
General suggestions for its implementation
When guiding the tasks, it is suggested to specify what they should do, their intention, the specific objective and the ways, means and possible strategies that promote creative learning. It is also necessary to highlight what each task contributes to professional training and how it stimulates the production of subjective meanings.
During the PEA, it is recommended that the teacher and students exchange systematically and that communication is mediated by respect for divergent opinions, innovation, knowledge production, cooperative work, criticism, collaboration, discussion and defend your own ideas.
Likewise, the teacher must control the process and the result of each task. In this sense, one must be flexible and pay attention to the development of the skill and the forms of learning used. The class should favor the development of creativity, promote reflection and provide heuristic impulses that encourage the student to reflect.
When evaluating the fulfillment of the objective, the teacher must value the effort and the own production of the students and encourage their feedback. By promoting reflection on the solution paths used and the relevance of using different mathematical resources, depending on the chosen path, the treatment of errors and their causes will be enhanced.
On the other hand, a favorable learning climate must be promoted, where students demonstrate confidence, security and empathy. For this, it is suggested to encourage curiosity, questioning, imagination, critical reflection on learning and on oneself.
When problematizing about the contents of the calculation of integrals, the student must develop his thinking, discover relationships, deduce consequences and define concepts. Also, you must identify the element that causes the intellectual difficulty or contradiction and define or formulate the new problem through the use of definite integrals. When formulating theoretical and practical questions associated with the contents of calculus of definite integrals, the student must reveal the necessary conditions to solve the problem and establish causal dependencies; in order to establish relationships between the known and the unknown.
When modeling problematic situations, typical of the profession, related to the calculation of definite integrals, the student must understand its meaning and apply it according to the conditions of the problem posed; allowing them to identify, formulate and solve new problems. The approach and verification of hypotheses for the solution of exercises and problems of calculus of definite integrals must allow the obtaining of new knowledge and the determination of new and original ways to demonstrate them.
By exposing and arguing the solution paths and the results of the tasks, students must demonstrate new procedures, propose alternative solution algorithms and justify them, as well as offer new solution paths to problems solved by others. Likewise, they must self-critically assess their performance and that of their peers.
Instrumentation and evaluation of the didactic strategy
The strategy is applied during the preparation and development of the Higher Mathematics I subject in the aforementioned career and the person in charge is the teacher of the subject; although it is suggested that teachers from the year group and the discipline group participate.
According to the typology of the strategy, it is necessary to clarify that students and teachers play a fundamental role, since actions related to teaching and learning are required. In the first two stages, the teacher's performance is prioritized, although some of the actions included require the participation of the students. The actions of the execution stage are specified when giving each class and other forms of organization previously planned. At this stage, students must assume an active participation.
Finally, the evaluation of the didactic strategy focuses on the improvement of its general conception and its actions; To do this, discussion groups will be held in the methodological groups and the experiences of the subject teacher will be systematized.
Also, the transformations that students achieve at the level of development of the ability to calculate definite integrals will be evaluated. For this, it is suggested to systematically observe their performance, review the documents and apply tests that reflect the solution of exercises and problems related to the calculation of definite integrals.
As part of the results, the effects of the application of the didactic strategy were described after analyzing the information collected from the instruments used to evaluate the level of development of the ability to calculate definite integrals, in the students selected as a research sample.
To measure the indicators, two instruments were used. The following graph illustrates their behavior, once the information from both has been triangulated.
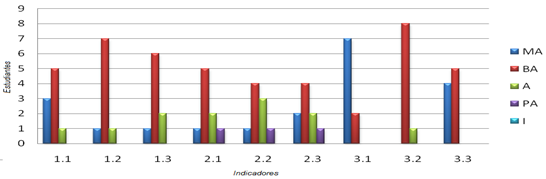
Graph 2- Triangulated analysis of the evaluated indicators (own elaboration).
Next, the quantitative analysis of each indicator is carried out (using for this the frequency and relative frequency) and it is argued, based on the qualitative evaluations that resulted from the collection and interpretation of information during the field work with the students, reflecting the following:
100% (9) knew the definition of indefinite integral and its meaning, properties and derivation rules; although they showed difficulties in the integration methods. In this sense, the students asked questions to their classmates and the teacher and set their own learning objectives.
88.9% (8) dominate the knowledge associated with indefinite integrals, the definition of definite integral and its meaning, as well as the fundamental theorem of integral calculus; demonstrating recognition of the meaning of these contents for their profession.
77.8% (7) knew the applications of the calculation of integrals to accounting and finance; the others did not understand the professional situations modeled by integral calculus. However, they were in favor of formulating or identifying problems specific to the profession that were resolved by applying this content.
88.9% (8) knew the procedure to calculate indefinite integrals and applied it correctly, although the analysis of the integrand was complex. The most frequent errors were when integrating functions by substitution and by parts that require repeating the procedure. On this matter, the students elaborated their own schemes and, when solving the exercises, they exchanged solution paths among themselves.
88.9% (8) correctly applied the actions of the procedure to calculate definite integrals, although they presented difficulties when determining the primitive of the function. They always applied the Fundamental Theorem of Integral Calculus and the Mean Value Theorem well.
88.9% (8) managed to apply the calculation of definite integrals to the solution of mathematical and professional problems, they were able to model professional situations and solve them and interpret the results from the perspective of accounting, evidencing varied ways of working and mathematical thinking.
100% were involved in the solution of the definite integral calculation tasks; they were active in solving them and believed that the study of these contents was important for their profession, as well as the argumentation of the process followed to reach the solution of the tasks.
100% (9) showed satisfaction with the solution of definite integral calculation tasks, since they achieved an improvement in the learning results.
100% (9) maintained a high disposition during the solution of definite integral calculation tasks, evidencing their interest in learning and considering it appropriate to develop some means or strategies for their own learning.
Finally, the authors refer that with the application of the didactic strategy it was possible for the students to use learning methods and means that stimulated their active participation and the elaboration of knowledge, the problematization and the contextualization of professional tasks; all this reflected in the transformations that could be verified and with a positive effect on the level of development of the ability to calculate definite integrals at the end of the experimentation.
DISCUSSION
The investigative process described in this article allows the authors to:
Signify the need and relevance of achieving the coherent integration of the theoretical conceptions that support the Teaching-Learning Process of Mathematics with a developer approach and the guidelines that characterize its methodological approach at any educational level; and highlight what is related to the use of various types of tasks that promote the transit of students through the different levels of assimilation, depending on the development of the specific mathematical ability that is worked on.
Establish relationships between the theoretical criteria of relevance for the Teaching-Learning Process of the calculation of integrals; That is why, for the development of the ability to calculate definite integrals, the use of problems, conceptual understanding, modeling and analysis of situations linked to the problems of the profession are prioritized.
Consider a novel finding, from the theoretical point of view, the particularities and demands of creative learning for the treatment of the calculation of integrals; since these can contribute to the integral formation of the students and, particularly, to the development of the ability that is studied by implying the integrated use of methods, means and strategies that stimulate different forms of learning.
Point out as a theoretical value of the article the enrichment of the Didactics of Mathematics, by referring in an integrated way to the conceptions of the Developer Teaching-Learning Process and its methodological requirements from the perspective of creative learning; as well as in the conceptualization that is made of the ability to calculate definite integrals and the generalized procedure for its development.
Describe as a practical value of the article the general conception of the didactic strategy and its actions, based on guiding the actions of teachers and students for the development of the mathematical ability that is studied; since this requires students to personalize information, confront what is given, problematize information and produce and generate their own ideas.
Point out that the results of the implementation of the didactic strategy reaffirm the possibility of socializing it and, in turn, perfecting it, since although higher levels of development of the ability to calculate definite integrals were achieved in the students with whom we worked, elements were identified that They can be improved to achieve a greater scope in this and other university careers.
BIBLIOGRAPHIC REFERENCES
Álvarez Pérez, M., Almeida Carazo, B. y Villegas Jiménez, E. V. (2014). El proceso de enseñanza-aprendizaje de la asignatura matemática documentos metodológicos. La Habana: Pueblo y Educación.
Ballester Pedroso, S., García La Rosa, J. E., Almeida Carazo, B., Álvarez Pérez, M., Rodríguez Ortiz, M., González Noguera, R. A., Villegas Jiménez, E. V., Fonseca González, A. L. y Puig Reyes, N. (2018). Didáctica de la Matemática (Tomo 1). La Habana: Pueblo y Educación.
Ferrer Vicente, M. y Rebollar Morote, A. (1995). Cómo dirigir el proceso de formación de habilidades matemáticas [Curso]. Curso impartido en el Evento Internacional Pedagogía 1995. La Habana: Cuba.
Fonseca Castro, J. L., y Alfaro Carvajal, C. R. (2018). El cálculo diferencial e integral en una variable en la formación inicial de docentes de matemática en Costa Rica. Revista Educación, 42(2), 1-22. https://revistas.ucr.ac.cr/index.php/educacion/article/view/25844
Granera Rugama, J. A. (2019). La integral definida como el área bajo una curva en un entorno computacional. Revista Científica de FAREM-Estelí, 8(30). https://dialnet.unirioja.es/descarga/articulo/7304343.pdf
Martínez Castellini, A. (2020). Uso de métodos problémicos en el proceso de enseñanza aprendizaje de la matemática: metodología para calcular integrales indefinidas. Revista Universidad y Sociedad, 12(5), 445-453. https://rus.ucf.edu.cu/index.php/rus/article/view/1731
Mitjáns Martínez, A. (2013). Aprendizaje creativo: desafíos para la práctica pedagógica. Revista CS, 11. https://doi.org/10.18046/recs.i11.1574
Rodríguez del Castillo, M. A. y Rodríguez Palacios, A. (2011). La estrategia como resultado científico de la investigación educativa. En N. De Armas Ramírez y A. Valle Lima (Eds.), Resultados científicos en la investigación educativa. (pp. 20-51). Pueblo y Educación: Cuba.
Rojas Taño, A. y Rodríguez Sosa, J. B. (2021). La significatividad del aprendizaje del cálculo diferencial e integral. VARONA. Revista Científico Metodológica, 72(enero-junio), 11-15. http://revistas.ucpejv.edu.cu/index.php/rVar/article/download/1135/1513
Sánchez Companioni, W., Pérez González, A. y Remedios González, J. M. (2022). El aprendizaje creativo: una alternativa para el proceso de enseñanza y aprendizaje de la Matemática. Pedagogía y Sociedad, 25 (63), 312-331. http://revistas.uniss.edu.cu/index.php/pedagogia-y-sociedad/article/view/1278
Suárez Rincón, M. L. (2018). Estrategias pedagógicas para la enseñanza de las matemáticas en Administración: Estudios y experiencias. Revista Electrónica Interuniversitaria de Formación del Profesorado, 21(2), 79-89. DOI: https://doi.org/10.6018/reifop.21.2.323261
Rodríguez Saltos, E. R., Vallejo Loor, B. M., Yenchong Meza, W. E., y Ponce Solórzano, M. J. (2020). Importancia de la psicopedagogía y el aprendizaje creativo. Dominio de las Ciencias, 6(3), 564-581. http://dx.doi.org/10.23857/dc.v6i3.1300
Villena Muñoz, M., y Rivas Maldonado, N. (2019). Impacto del uso de la tecnología en el proceso de enseñanza- aprendizaje del cálculo integral. Revista Conrado, 15(68), 297-307. https://conrado.ucf.edu.cu/index.php/conrado/article/view/1028Villenas
Conflict of interests:
The authors declare not to have any interest conflicts.
Contribution of the authors:
The authors participated in the design and writing of the work, and analysis of the documents.
![]()
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0
International License
Copyright (c) Wilfredo Sánchez Companioni , Andel Pérez González & Juana María
Remedios González.