
Mendive. Revista de Educación, 21(1), e3007
Artículo original
Estrategia didáctica para desarrollar la habilidad calcular integrales definidas desde un aprendizaje creativo
Didactic strategy to develop the ability to calculate definite integrals from creative learning
Estratégia didática para desenvolver a capacidade de calcular integrais definidas a partir do aprendizado criativo
Wilfredro Sánchez Companioni1 ![]() http://orcid.org/0000-0002-3033-9430
http://orcid.org/0000-0002-3033-9430
Andel Pérez González1 ![]() http://orcid.org/0000-0003-4435-4030
http://orcid.org/0000-0003-4435-4030
Juana María Remedios González1 ![]() http://orcid.org/0000-0001-7030-5326
http://orcid.org/0000-0001-7030-5326
1Universidad de Sancti Spíritus José Martí Pérez. Cuba
![]() wilfredosc@uniss.edu.cu, apgonzalez@uniss.edu.cu, jremedios@uniss.edu.cu
wilfredosc@uniss.edu.cu, apgonzalez@uniss.edu.cu, jremedios@uniss.edu.cu
| Sánchez Companioni, W., Pérez González, A., & Remedios González, J. (2023). Estrategia didáctica para desarrollar la habilidad calcular integrales definidas desde un aprendizaje creativo. Mendive. Revista de Educación, 21(1), e3007. https://mendive.upr.edu.cu/index.php/MendiveUPR/article/view/3007 |
Recibido: 31 de marzo 2022.
Aceptado: 27 de octubre 2022.
RESUMEN
El desarrollo de habilidades en la formación de los profesionales universitarios constituye una temática de gran actualidad; sobre todo, si se tiene en cuenta que en ellas se expresa el saber hacer de los estudiantes y su relación con el mundo laboral para el que se preparan. De ahí, la importancia de desarrollar la habilidad calcular integrales definidas en los estudiantes de la carrera Licenciatura en Contabilidad y Finanzas; ya que esta facilita la solución de diversas situaciones propias de la profesión. Es por ello que, este artículo tuvo como objetivo socializar una estrategia didáctica dirigida al desarrollo de la habilidad calcular integrales definidas, desde un Proceso de Enseñanza-Aprendizaje creativo de la asignatura Matemática Superior I. Para su diseño se utilizó una metodología cuantitativa que exigió el empleo de métodos teóricos como el histórico-lógico, el analítico-sintético y el inductivo-deductivo, los que hicieron posible la fundamentación teórica de la estrategia didáctica; así como los empíricos: revisión del producto de la actividad y la observación, para conocer el nivel de desarrollo de la habilidad en los estudiantes que participaron en la investigación. El principal resultado lo constituyó, precisamente, la estrategia didáctica y las sugerencias metodológicas para su implementación. Su aplicación en la práctica evidenció transformaciones favorables en el nivel de desarrollo de la habilidad objeto de análisis; reafirmándose así su factibilidad y, sobre todo, la pertinencia del aprendizaje creativo.
Palabras clave: creatividad; estrategia didáctica; habilidad; calcular integrales definidas; aprendizaje creativo y matemática.
ABSTRACT
The development of abilities in the formation of the university professionals constitutes a thematic of great present time; mainly, if one keeps in mind that in them the knowledge is expressed to make of the students and its relationship with the labor world for which you/they get ready. Of there, the importance of developing the ability to calculate integrals defined in the students of the career Degree in Accounting and Finances; since this it facilitates the solution of diverse situations characteristic of the profession. It is for it that, this article had as objective to socialize a didactic strategy directed to the development of the ability to calculate defined integrals, from a process of creative teaching-learning of the Superior Mathematical subject I. For its design a quantitative methodology was used that demanded the employment of theoretical methods as the historical-logical one, the analytic-synthetic one and the inductive-deductive one; those that made possible the theoretical foundation of the didactic strategy; as well as the empiric ones: revision of the product of the activity and the observation, applied to know the level of development of the ability in the students that participated in the investigation. The main result, in fact constituted it the didactic strategy and the methodological suggestions for its implementation. Its application in the practice evidenced favorable transformations in the level of development of the ability analysis object; being reaffirmed this way their feasibility and, mainly, the relevancy of the creative learning.
Keywords: creativity; didactic strategy; ability; to calculate defined integrals; creative learning and mathematics.
RESUMO
O desenvolvimento de competências na formação de profissionais universitários é um tema de grande relevância; sobretudo, se tivermos em conta que expressam o saber-fazer dos alunos e a sua relação com o mundo do trabalho para o qual estão a preparar-se. Daí a importância de desenvolver a capacidade de calcular integrais definidas nos alunos da carreira de Bacharel em Contabilidade e Finanças; já que isso facilita a solução de diversas situações da profissão. É por isso que este artigo teve como objetivo socializar uma estratégia didática que visa desenvolver a capacidade de calcular integrais definidas, a partir de um processo criativo de Ensino-Aprendizagem da disciplina de Matemática Superior I. Para seu desenho, foi utilizada uma metodologia quantitativa que exigiu o uso de métodos como o histórico-lógico, o analítico-sintético e o indutivo-dedutivo, que possibilitaram a fundamentação teórica da estratégia didática; bem como os empíricos: revisão do produto da atividade e observação, para conhecer o nível de desenvolvimento de habilidades nos alunos que participaram da pesquisa. O principal resultado foi justamente a estratégia didática e as sugestões metodológicas para sua implementação. Sua aplicação na prática evidenciou transformações favoráveis no nível de desenvolvimento da habilidade em análise; reafirmando assim a sua viabilidade e, sobretudo, a relevância da aprendizagem criativa.
Palavras-chave: criatividade; estratégia didática; habilidade; calcular integrais definidas; aprendizagem criativa e matemática.
INTRODUCCIÓN
La economía, la cultura y las políticas sociales a nivel internacional y nacional, en la actualidad, se caracterizan por sucesivas transformaciones que responden al rápido progreso de la ciencia, la técnica y la tecnología; así como a las demandas de la sociedad. En este sentido, la educación universitaria debe asegurar la formación de profesionales competentes, capaces de asumir los retos del presente y el futuro.
Al respecto, el Ministerio de Educación Superior en Cuba (MES), consciente de su responsabilidad en el perfeccionamiento constante del proyecto social cubano, tiene como prioridad la mejora continua del proceso de formación de los profesionales universitarios. Sobre este particular, se precisa que la universidad debe distinguirse por la formación de valores y por el aseguramiento de la calidad de sus procesos sustantivos, en aras de lograr un egresado que posea cualidades personales, cultura y habilidades profesionales que le permitan desempeñarse con responsabilidad social.
Ante esta exigencia, el Proceso de Enseñanza-Aprendizaje (PEA) en las universidades debe propiciar la formación y el desarrollo de las habilidades necesarias para cumplir las funciones profesionales propias de cada carrera. Solo así, sus egresados conseguirán una mejor inserción en las dinámicas sociales y productivas de la profesión. Es por ello que se analiza el Proceso de Enseñanza-Aprendizaje de la Matemática, como:
Un proceso en el cual tanto la enseñanza como el aprendizaje son subsistemas que garantizan la apropiación activa, creadora, reflexiva, significativa y motivada del contenido como parte de la cultura general integral, teniendo en cuenta el desarrollo actual, con el propósito de ampliar continuamente los límites de la zona de desarrollo próximo potencial. Ello implica una comunicación afectiva y el desarrollo de actividades intencionales, cuyo accionar didáctico genere estrategias de aprendizaje que permitan aprender a aprender Matemática, como expresión del desarrollo constante de una personalidad integral y autodeterminada del estudiante (Ballester Pedroso, García La Rosa, Almeida Carazo, Álvarez Pérez, Rodríguez Ortiz, González Noguera, Villegas Jiménez, Fonseca González, y Puig Reyes, 2018, p. 13).
Desde esta perspectiva, la preparación de los estudiantes para aplicar los conocimientos matemáticos a la solución de los problemas profesionales propios de la contabilidad y las finanzas se identifica como una tarea compleja. De ahí, que se le asigne un rol fundamental al aprendizaje de los contenidos que se relacionan con el cálculo de integrales definidas, por lo que aportan a la comprensión y solución de problemáticas de la Licenciatura en Contabilidad y Finanzas (Sánchez Companioni, Pérez González y Remedios González, 2022) y, en particular, a la formación y desarrollo de las habilidades correspondientes. De ahí que se asuma la definición de Ferrer Vicente y Rebollar Morote (1995), donde refieren que:
Una habilidad matemática es la construcción, por el alumno, del modo de actuar inherente a una determinada actividad matemática, que le permite buscar o utilizar conceptos, propiedades, relaciones, procedimientos matemáticos, utilizar estrategias de trabajo, realizar razonamientos, juicios que son necesarios para resolver problemas matemáticos (p. 5).
Al profundizar en el Proceso de Enseñanza-Aprendizaje del cálculo de integrales definidas, Suárez Rincón (2018) subraya la pertinencia de valerse de recursos novedosos que faciliten la comprensión de los conceptos y el desarrollo de las habilidades matemáticas específicas de este tema; en consecuencia, la habilidad calcular integrales definidas se considera como: la operación mediante la cual se obtiene el valor del área determinada entre la curva que determina la función y un segmento de eje coordenado determinado por un intervalo [a,b], en el cual dicha curva es integrable. Dicho valor resulta del cálculo de la primitiva correspondiente a la expresión analítica de la curva y la aplicación de la fórmula fundamental del cálculo integral.
En consecuencia, se utiliza un procedimiento general para trabajar la formación y el
desarrollo de la habilidad calcular integrales indefinidas que resume las acciones que deben dominar
los estudiantes. El mismo implica: el análisis del integrando para decidir si la integral es
inmediata o no (si se calcula su primitiva utilizando solo las propiedades y reglas de integración o si
se necesita, además, de algún método de integración); si la integral es inmediata, se
identifican las propiedades de la integral indefinida y las reglas de integración a utilizar y si es
inmediata se selecciona el método de integración a utilizar; se calcula la primitiva de la función
f(x): F(x); se aplica la fórmula fundamental del cálculo integral ![]() ; se calculan los valores numéricos de F (b)= B y F (a) = A; A,B
; se calculan los valores numéricos de F (b)= B y F (a) = A; A,B ![]() y se calcula el valor de
y se calcula el valor de
![]() .
.
Por otra parte, Fonseca Castro y Alfaro Carvajal (2018) manifiestan la utilidad de utilizar la modelización, la resolución de problemas y las herramientas tecnológicas como estrategias de aprendizaje. Igualmente, para Villena Muñoz y Rivas Maldonado (2019) resulta pertinente dominar los procedimientos de cálculo y aplicarlos a la solución de problemas. Mientras que Granera Rugama (2019) señala que aprender los contenidos del cálculo de integrales definidas significa comprender el significado de los conceptos, dominar los procedimientos y desarrollar las habilidades propias del cálculo; referente a ello prioriza la utilización de métodos de enseñanza que propicien el desarrollo del pensamiento matemático avanzado y el uso de las tecnologías.
De igual forma, Martínez Castellini (2020) opina que, al no existir un procedimiento para calcular integrales, las tareas docentes adquieren la connotación de problema; lo que justifica la utilización de métodos que propicien la reflexión, la actividad productiva y el desarrollo del pensamiento creador de los estudiantes y, en ese sentido, Rojas Taño y Rodríguez Sosa (2021) resaltan el valor de contextualizar los contenidos a las problemáticas de cada carrera.
Estas ideas se relacionan o complementan al ser consecuentes con el aprendizaje creativo; visto este como:
Una forma de aprender que se diferencia de las formas de aprendizaje comunes en el medio escolar, y se caracteriza por el tipo de producción que el aprendiz hace y por los procesos subjetivos en ella implicados (…) Este aprendizaje tiene diferentes formas de expresión y en él participan un conjunto de recursos subjetivos y se expresa en la configuración, como mínimo de tres procesos: la personalización de la informatización, la confrontación con lo dado y la producción de ideas propias y nuevas (Mitjáns Martínez, 2013, p. 317).
A pesar de ello, aunque de forma general en los trabajos consultados se abordan aristas de interés para el Proceso de Enseñanza-Aprendizaje de las integrales definidas, no fue posible encontrar estudios específicos que focalizaran su atención en el desarrollo de la habilidad calcular integrales definidas. En consecuencia, en este artículo se reflexiona en torno a la siguiente interrogante: ¿qué vía se puede utilizar para contribuir al desarrollo de la habilidad calcular integrales definidas desde el PEA de la asignatura Matemática Superior I?
En tanto, como respuesta a la interrogante anterior, los autores se plantean como objetivo socializar una estrategia didáctica que contribuya al desarrollo de la habilidad calcular integrales definidas, desde un Proceso de Enseñanza-Aprendizaje creativo de la asignatura Matemática Superior I.
Su importancia radica en que pone a consideración de los profesores de matemática una vía diferente para potenciar el desarrollo de la habilidad calcular integrales definidas; en este caso, desde las particularidades del aprendizaje creativo. Su alcance está dado por lo que puede significar para el desarrollo de la habilidad referida en los estudiantes de la Licenciatura en Contabilidad y Finanzas y en otras carreras universitarias; así como por la posibilidad de transferir lo relativo al aprendizaje creativo a otros contenidos matemáticos.
MATERIALES Y MÉTODOS
Para responder la interrogante que se plantearon los autores, fue necesario utilizar una metodología cuantitativa que facilitara la utilización de métodos teóricos y empíricos.
De los teóricos, se utilizó el histórico-lógico, el analítico-sintético y el inductivo-deductivo; los que permitieron determinar las posiciones teóricas en torno al PEA de la Matemática y, en particular, de las integrales definidas y del aprendizaje creativo. Igualmente, facilitaron el estudio de las habilidades matemáticas y su desarrollo.
Por otra parte, fue preciso recurrir al análisis del producto de la actividad y a la observación como métodos empíricos; los que hicieron posible profundizar en el estudio del nivel de desarrollo de la habilidad matemática calcular integrales definidas en los estudiantes participantes de la investigación. Se observó el desempeño de los estudiantes durante la solución de diferentes tipos de tareas que exigían el cálculo de integrales definidas utilizadas en las clases prácticas. Con igual intención, se revisaron las notas que describían la solución de las tareas resueltas en los cuadernos de la asignatura, las evaluaciones escritas y en otros trabajos de clases.
De ahí, que se determinará como unidad de análisis a los estudiantes de la Licenciatura en Contabilidad y Finanzas de la Universidad de Sancti Spíritus "José Martí Pérez"; la población estuvo integrada por los 34 estudiantes de la referida carrera y los nueve estudiantes de primer año formaron parte de la muestra con que se trabajó durante la aplicación de la estrategia didáctica, por ser este el momento donde se impartía el contenido que se estudia.
Para el procesamiento de la información resultante del diagnóstico y de la implementación de la estrategia didáctica, se utilizaron métodos estadístico-matemáticos; en particular, la estadística descriptiva y, de ella, las medidas de tendencia central y la representación gráfica para su mejor interpretación. Por otra parte, se utilizó la triangulación metodológica para lograr una mayor objetividad y credibilidad del análisis de la información que se obtuvo de la aplicación de los métodos empíricos antes descritos.
RESULTADOS
Se inicia este apartado con los resultados del diagnóstico del nivel de desarrollo de la habilidad calcular integrales definidas en los estudiantes que seleccionados de la población. Estos, permitieron valorar como posible vía de solución a la problemática planteada el diseño de una estrategia didáctica.
Al asumir como objeto a evaluar el desarrollo de la habilidad calcular integrales definidas, se precisaron indicadores cognitivos, procedimentales y actitudinales que se derivan de las posiciones teóricas asumidas en la introducción del artículo. Los cognitivos reflejan los conocimientos esenciales para lograr el desarrollo de la habilidad correspondiente y su necesaria comprensión por parte de los estudiantes, estos fueron: el dominio de los conocimientos necesarios para el cálculo de integrales indefinidas (1) y definidas respectivamente (2); así como los conocimientos profesionales relacionados con las integrales definidas (3). Los procedimentales particulares incluyen, en cada uno de los dos, las acciones y operaciones que debían saber hacer los estudiantes para calcular integrales definidas, ellos fueron: la aplicación del procedimiento asociado al cálculo de integrales indefinidas (4); la aplicación del procedimiento asociado al cálculo de integrales definidas (5) y la aplicación del cálculo de integrales definidas a la solución de problemas profesionales (6).
En tanto, las actitudes evaluadas fueron: la implicación (7), la satisfacción (8) y la disposición (9) de los estudiantes durante la solución de tareas de cálculo de integrales definidas.
Para la medición, se utilizaron los métodos empíricos precisados en la introducción y una escala ordinal que consideraba las categorías de Muy Adecuada (MA), Bastante Adecuada (BA), Adecuada (A), Poco Adecuada (PA) e Inadecuada (I).
La gráfica 1 muestra los resultados, luego de observar el desempeño de los estudiantes durante el desarrollo de las clases prácticas y de revisar los productos elaborados por ellos en cuadernos y evaluaciones escritas de cálculo de integrales definidas.
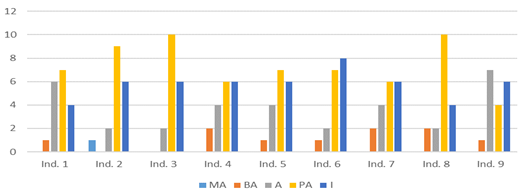
Gráf. 1- Resultados de los indicadores evaluados (elaboración propia)
El análisis cualitativo de los resultados evidenció que los estudiantes:
Conocían la definición de integral indefinida, pero sin llegar a comprender su significado, e identificaban las propiedades y reglas de integración de las funciones elementales.
Reconocían los métodos de integración, pero no comprendían sus pasos y tampoco las condiciones necesarias y suficientes del teorema fundamental y del valor medio.
Generalmente, no priorizaban el análisis de lo profesional en los ejercicios de aplicación y solo se concentraban en lo relativo a la matemática.
Conocían las acciones para calcular integrales indefinidas, pero no realizaban un análisis del integrando. En ocasiones elegían bien el método, pero no dominaban sus acciones.
Con frecuencia, cometían errores al aplicar los métodos de integración, al determinar la primitiva y al utilizar el teorema fundamental del cálculo integral y del valor medio.
Casi nunca lograban modelar las situaciones problémicas relacionadas con la profesión y en ningún caso profundizaron en el significado profesional de ellas.
No siempre se mostraron activos al realizar las tareas, no las consideraban importantes para su profesión y tampoco generaban ideas y vías de solución propias.
Se mostraban insatisfechos, pues con frecuencia cometían errores y tampoco comprendían el contenido y su aplicación práctica a la profesión.
Los resultados descritos evidenciaron una contradicción entre estado real de desarrollo de la habilidad calcular integrales definidas y el exigido. De ahí, la necesidad de diseñar una estrategia didáctica que permitiera transformar dicha realidad, la cual se describe a continuación.
La estrategia didáctica que se socializa, parte de considerar las posiciones teóricas de Rodríguez del Castillo y Rodríguez Palacios (2011) y las experiencias que orientan el cumplimiento de un objetivo y permiten la organización, planificación, ejecución y evaluación del PEA. De ahí que se asuma la estrategia didáctica como la proyección de un sistema de acciones a corto, mediano y largo plazos, que permite la transformación del Proceso de Enseñanza-Aprendizaje en una asignatura, nivel o institución tomando como base los componentes del mismo y que permite el logro de los objetivos propuestos en un tiempo concreto (Rodríguez del Castillo y Rodríguez Palacios, 2011, p. 39).
En consecuencia, se siguen sus criterios en relación a la estructura de la estrategia; esta precisa sus fundamentos teóricos, su objetivo general y sus etapas contentivas de objetivos específicos, acciones y sugerencias para su realización, así como las orientaciones que guían su instrumentación y evaluación.
Los fundamentos de la estrategia didáctica se organizaron en tres direcciones: el Proceso de Enseñanza-Aprendizaje de la Matemática, el desarrollo de la habilidad matemática calcular integrales definidas y el aprendizaje creativo.
En la primera dirección, se significa el enfoque desarrollador del Proceso de Enseñanza-Aprendizaje de la Matemática y se consideran como sus dimensiones la activación-regulación, la significatividad y la motivación (Ballester Pedroso, García La Rosa, Almeida Carazo, Álvarez Pérez, Rodríguez Ortiz, González Noguera, Villegas Jiménez, Fonseca González, y Puig Reyes, 2018) y, en relación a ellas, se afirma que para el desarrollo de la habilidad objeto de análisis es necesario que los estudiantes dominen los conceptos, proposiciones, procedimientos, técnicas, estrategias de trabajo y desarrollo de sentimientos, actitudes y valores; que identifiquen los diferentes tipos de tareas de aprendizaje, las estrategias para su solución y los mecanismos de control para la corrección de las tareas y, en particular, que se apropien del procedimiento general trabajado en la introducción; así como, establecer relaciones entre los nuevos conocimientos con los anteriores y con los de otras asignaturas y reconstruir sus formas de pensar y actuar en diferentes contextos de aprendizaje profesional.
También se le atañe un valor significativo a la exigencia que explicita lo relativo al desarrollo de la creatividad desde el enfoque metodológico del PEA de la Matemática. Esta precisa la necesidad de "potenciar el desarrollo hacia niveles superiores de desempeño, a través de la realización de tareas de carácter interdisciplinario y el tránsito progresivo de la dependencia a la independencia y la creatividad" (Álvarez Pérez, Almeida Carazo y Villegas Jiménez, 2014, p. 1).
Se insiste en la necesidad de que los estudiantes se motiven y activen durante la realización de tareas variadas, en la pertinencia de utilizar las tecnologías con fines heurísticos para que logren adquirir conocimientos y racionalicen el trabajo mental y en la importancia de que interactúen, reflexionen y cooperen entre ellos al resolver las tareas de aprendizaje (Álvarez Pérez, Almeida Carazo y Villegas Jiménez, 2014) relacionadas con el cálculo de integrales.
Por otra parte, se precisan los elementos teóricos de interés para el PEA de las integrales definidas, desde las relaciones entre los componentes del PEA.
Desde el objetivo, hay que puntualizar la necesidad de que el PEA de las integrales definidas potencie el desarrollo del pensamiento lógico de los estudiantes y su formación integral (Granera Rugama, 2019). En tanto, se deben destacar los conocimientos y habilidades esenciales que este contenido aporta para su desarrollo profesional (Fonseca Castro y Alfaro Carvajal, 2018) y, sobre todo, los procedimientos a utilizar en cada caso del cálculo de integrales y sus vínculos con las disciplinas de la profesión.
En tanto, para el Proceso de Enseñanza-Aprendizaje de estos contenidos se deben utilizar métodos que propicien el desarrollo del pensamiento matemático (Granera Rugama, 2019) y que favorezcan la formulación de conjeturas, los procesos inductivos y la argumentación (Fonseca Castro y Alfaro Carvajal, 2018) de las acciones y operaciones necesarias para el desarrollo de la habilidad.
Igualmente, es preciso seleccionar medios que permitan modelar situaciones problemáticas, propiciar el tránsito hacia la independencia cognoscitiva de los estudiantes y estimulen la integración entre profesor-alumno-conocimiento-tecnología y con el contexto (Villena Muñoz y Rivas Maldonado, 2019), destacándose como esencial el uso de las TIC.
Particularmente, se enfatiza en los tipos de tareas como parte de las formas de organización; las cuales deben exigir el planteamiento y la solución de problemas contextualizados, donde sea necesario la modelación matemática y el uso de estrategias que estimulen la participación activa de los estudiantes para su solución desde un aprendizaje significativo (Rojas Taño y Rodríguez Sosa, 2021).
Según lo anterior, se precisan las exigencias para lograr aprendizajes creativos del cálculo de integrales definidas en estudiantes de la carrera Contabilidad y Finanzas:
Plantearse objetivos de aprendizaje para el estudio de los contenidos matemáticos y metas individualizadas para su cumplimiento.
Atribuir significado a los conocimientos y habilidades matemáticas (conceptos, proposiciones, procedimientos, estrategias de trabajo matemático, habilidades).
Establecer relaciones entre los conocimientos y habilidades matemáticas con los contenidos antecedentes y de otras asignaturas.
Identificar, formular y resolver problemas matemáticos, de otras ciencias o de la vida práctica donde sea necesario la aplicación de los contenidos matemáticos.
Actuar con motivación, independencia cognoscitiva y originalidad durante la búsqueda de variadas vías de solución a las tareas que exigen de la aplicación de los contenidos matemáticos en diferentes contextos.
Utilizar métodos de aprendizaje que propicien su participación independiente, original y motivada durante la aplicación de los conocimientos y habilidades matemáticas en diferentes contextos.
Utilizar procedimientos que propicien el desarrollo de las formas de trabajo y de pensamiento matemático durante la aplicación de los conocimientos y habilidades matemáticas en diferentes contextos.
Utilizar o elaborar medios de aprendizaje que faciliten la aplicación de los conocimientos y habilidades matemáticas en diferentes contextos.
Exponer, argumentar y evaluar sus vías de solución a las tareas y las de sus compañeros.
Establecer relaciones con sus compañeros y con el profesor, en un clima de agrado y colaboración (Sánchez Companioni, Pérez González y Remedios González, 2022, 325-326).
La segunda dirección retoma los elementos en que se fundamenta el trabajo con la habilidad matemática que se pretende desarrollar con la estrategia didáctica y presta atención a las condicionantes metodológicas a seguir para el desarrollo de una habilidad: el trabajo, primero con ejecuciones simples y después más complejas, graduar la periodicidad temporalmente de las acciones y las operaciones, aplicar la habilidad en varios contextos, exigir el perfeccionamiento continúo de las acciones y operaciones que determinan la habilidad y fomentar la motivación de los estudiantes por la realización consciente de los diferentes tipos de tareas en que se utiliza la habilidad.
Por último, la tercera dirección tiene que ver con el aprendizaje creativo. Al respecto, se considera la creatividad como su forma de expresión fundamental y este debe potenciar la producción de sentidos y configuraciones subjetivas (Mitjáns Martínez, 2013); de ahí, que resulte esencial la manera de concebir y realizar la enseñanza. La propia autora insiste en la necesidad de priorizar la producción de ideas novedosas, así como de ofrecer la posibilidad al estudiante de ir más allá de lo establecido y que se implique en la producción de sus recursos propios para aprender a realizar las acciones y operaciones que corresponden al cálculo de integrales definidas.
Además, se tiene en cuenta que aprender creativamente es expresarse diferente, ya que cada estudiante posee su propio pensamiento acerca de las cosas en el ámbito escolar y que el aprendizaje creativo estimula la solución a un problema a partir de la experiencia y destaca la idea de que pueden existir múltiples soluciones.
En tanto, se destacan como vías que lo estimulan: la construcción del conocimiento, la colaboración, la comunicación, el uso de las tecnologías de la información y las comunicaciones, la autoevaluación, la solución innovadora de problemas reales y el cuestionamiento (Rodríguez Saltos, Vallejo Loor, Yenchong Meza y Ponce Solórzano, 2020).
Además, sus procesos subjetivos se analizan desde las posiciones de la propia Mitjáns Martínez (2013), cuando explica que la personalización de la información ocurre al adquirir significado para los estudiantes; es decir, cuando la información asimilada se transforma al operar con ella en condiciones y contextos diferentes. También, cuando la confrontación con lo dado implica el cuestionamiento y la problematización de la información; la no aceptación de lo dado como única alternativa y se identifican o se plantean contradicciones que estimulan la producción y generación de nuevas ideas. En tanto, la producción y generación de ideas propias sobre lo estudiado hace necesario que los estudiantes identifiquen nuevas opciones y se formulen hipótesis sobre el objeto que se estudia.
Al ser consecuente con lo anterior, la estrategia didáctica diseñada se distingue por promover aprendizajes creativos, lo cual se expresa en: la personalización de la información, la confrontación con lo dado, la problematización de la información y la producción y generación de ideas propias. La misma, se concibe a partir de que el PEA cumpla con las exigencias siguientes: utilizar los problemas matemáticos y profesionales para la adquisición y fijación del conocimiento; emplear las Tecnologías de la Información y las Comunicaciones (TIC) como medio para obtener información y generar aprendizajes; estimular el interés por la producción de conocimientos; potenciar la imaginación, la curiosidad, la problematización y la generación de ideas propias y fomentar la participación activa durante la realización de las tareas.
Luego, su objetivo general es contribuir al desarrollo de la habilidad calcular integrales definidas en los estudiantes de la Licenciatura en Contabilidad y Finanzas; de ahí que se incluyan acciones para profesores y estudiantes. Para su diseño se determinaron tres etapas interrelacionadas entre sí: diagnóstico, planeación y ejecución.
Etapa de diagnóstico
Objetivo: evaluar el dominio de los contenidos antecedentes necesarios para el desarrollo de la habilidad calcular integrales definidas y las condiciones para el logro de aprendizajes creativos en los estudiantes de la carrera.
Acciones a realizar: determinación de los contenidos antecedentes a evaluar y de las manifestaciones que evidencian aprendizajes creativos, elaboración de los instrumentos, aplicación de los instrumentos y análisis triangulado de sus resultados, determinación de las potencialidades y dificultades a considerar para el desarrollo de la habilidad calcular integrales definidas y proyección de acciones correctivas para solucionar las dificultades.
Sugerencias generales para la realización de las acciones
La determinación de los contenidos antecedentes exige revisar el programa de la disciplina y asignatura, así como otros textos y materiales docentes. En el caso de las manifestaciones de aprendizaje creativo se deben analizar las posiciones teóricas asumidas. Se sugiere utilizar instrumentos donde se logre interactuar con los estudiantes; es decir: la observación, la revisión del producto de la actividad y la entrevista. Previo a su aplicación, se necesita asegurar el compromiso de los estudiantes para que la información obtenida resulte más veraz y fiable. Sus resultados se analizan independiente y se triangulan para identificar regularidades; las problemáticas deben ser analizadas con los estudiantes, de modo que se impliquen en las acciones correctivas. Etapa de planificación
Objetivo: diseñar, a mediano y corto plazo, el proceso de formación y desarrollo de la habilidad calcular integrales definidas.
Acciones a realizar: formulación de los objetivos a cumplir, selección de los contenidos a desarrollar, determinación de los métodos, selección o diseño de medios de enseñanza, identificación de los tipos de tareas, diseño de vías de evaluación y selección de formas organizativas; en todos los casos se deben priorizar los que propicien aprendizajes creativos.
Sugerencias generales para la realización de las acciones
Los objetivos se derivan de los propuestos por la disciplina y asignatura, logrando explicitar su conexión con los problemas profesionales. Un ejemplo pudiera ser: resolver problemas de cálculo de integrales definidas, que permitan el análisis de situaciones propias de la Contabilidad y las Finanzas, mediante la aplicación de los diferentes métodos de integración.
Al determinar los contenidos se deben precisar los conocimientos, habilidades y actitudes profesionales a adquirir por los estudiantes. También, se identifican las formas de trabajo y de pensamiento y las estrategias más factibles para lograr aprendizajes creativos; de estas últimas constituyen ejemplos: la variación de condiciones y la búsqueda de relaciones.
La selección de los métodos debe priorizar los que estimulen la participación activa e independiente de los estudiantes; es decir: la exposición problémica, la búsqueda parcial o heurística o el investigativo. Los mismos, pueden integrar el aprendizaje basado en problemas o por proyectos y de los procedimientos heurísticos, dadas sus potencialidades para obtener soluciones originales. Al seleccionar los medios se priorizan los textos: Cálculo con trascendentes tempranas y Matemática Superior I y II; así como el Geogebra y el Derive.
En tal sentido, las guías de estudio deben incluir tareas variadas y que impliquen el uso de estrategias que propicien el logro de aprendizajes creativos. Los tipos de tareas a utilizar son: identificación y formulación de problemas propios de la contabilidad, cálculo de integrales definidas de forma inmediata, cálculo de integrales definidas aplicando los diferentes métodos de integración y resolución de problemas cuya solución exige el cálculo de integrales definidas.
Al diseñarlas, es preciso tener en cuenta su objetivo, que integren conocimientos y habilidades matemáticas y profesionales y que propicien formas de actuar propias del aprendizaje creativo. Igualmente, deben ofrecer la posibilidad de profundizar ilimitadamente en el estudio de los contenidos y sus aplicaciones profesionales; incitar a la reflexión; estimular las posibilidades de elección, la toma de decisiones y la autovaloración por parte de los estudiantes; así como el incremento gradual de su complejidad y grado de dificultad.
Las vías y formas de evaluación deben exigir el dominio de los conocimientos y su aplicación; propiciar la elaboración y comprobación de hipótesis, la problematización, el cuestionamiento durante la solución de los ejercicios y problemas. También hay que priorizar la realización de trabajos investigativos que estimulen la producción de conocimientos en estrecho vínculo con el perfil del profesional de la carrera.
Las formas de organización a emplear deben potenciar el logro de un aprendizaje creativo; es decir, propiciar que los estudiantes busquen, reflexionen, elaboren sus propias teorías y, sobre todo, lo hagan de forma autónoma. Se sugiere desarrollar diferentes tipos de clases, tutorías, prácticas de estudio y consultas.
Etapa de ejecución
Objetivo: impartir las clases que corresponden al proceso de formación y desarrollo de la habilidad calcular integrales definidas.
Acciones a realizar por los profesores: orientación de las tareas a realizar en la clase u otras formas de organización, desarrollo de intercambios sistemáticos con los estudiantes, control del proceso de solución y del resultado de las tareas, evaluación del cumplimiento del objetivo por parte de los estudiantes y creación de un clima favorable durante el aprendizaje.
Acciones generales a realizar por los estudiantes: problematización de los contenidos relacionados con el cálculo de integrales, formulación de preguntas asociadas al contenido, modelación de problemáticas de la profesión, planteamiento y comprobación de hipótesis asociadas a la solución de ejercicios y problemas de cálculo de integrales definidas, exposición y argumentación de vías de solución y de los resultados obtenidos, así como valoración crítica y autocrítica de las vías de solución y de los resultados.
Acciones específicas a realizar por los estudiantes: identificación y formulación de problemas o situaciones profesionales donde tomen sentido las integrales definidas, elaboración y aplicación de procedimientos para el cálculo de integrales definidas, elaboración y aplicación de un programa heurístico particular para la solución de problemas de cálculo de integrales definidas, elaboración de un material contentivo de situaciones profesionales que se resuelven mediante el cálculo de integrales definidas.
Sugerencias generales para su realización
Al orientar las tareas se sugiere precisar el qué deben hacer, su intención, el objetivo específico y las vías, medios y posibles estrategias que propician aprendizajes creativos. Hay que destacar, también, lo que cada tarea aporta a la formación profesional y cómo estimula la producción de sentidos subjetivos.
Durante el PEA, se recomienda que el profesor y los estudiantes intercambien sistemáticamente y que la comunicación esté mediada por el respeto a las opiniones divergentes, a la innovación, la producción de conocimientos, el trabajo cooperativo, la crítica, la colaboración, la discusión y la defensa de ideas propias.
Igualmente, el profesor debe controlar el proceso y el resultado de cada tarea. En este sentido, se debe ser flexible y prestar atención al desarrollo de la habilidad y a las formas de aprendizaje utilizadas. La clase debe favorecer el desarrollo de la creatividad, potenciar la reflexión y brindar impulsos heurísticos que inciten al estudiante a reflexionar.
Al evaluar el cumplimiento del objetivo, el profesor debe valorar el esfuerzo y la producción propia de los estudiantes y propiciar su retroalimentación. Al promover la reflexión sobre las vías de solución empleadas y la pertinencia de emplear diferentes recursos matemáticos, según el camino elegido, se potenciará el tratamiento a los errores y sus causas.
Por otra parte, hay que potenciar un clima favorable de aprendizaje, donde los estudiantes demuestren confianza, seguridad y empatía. Para ello, se sugiere incentivar la curiosidad, el cuestionamiento, la imaginación, la reflexión crítica sobre el aprendizaje y sobre sí mismo.
Al problematizar acerca de los contenidos del cálculo de integrales, el estudiante debe desarrollar su pensamiento, descubrir relaciones, deducir consecuencias y definir conceptos. También, deberá identificar el elemento que provoca la dificultad intelectual o contradicción y definir o formular el nuevo problema mediante el uso de las integrales definidas. Al formular preguntas teóricas y prácticas asociadas a los contenidos de cálculo de integrales definidas, el estudiante debe revelar las condiciones necesarias para resolver el problema y establecer dependencias causales; para así establecer relaciones entre lo conocido y lo desconocido.
Al modelar situaciones problemáticas, propias de la profesión, relacionadas con el cálculo de integrales definidas, el estudiante debe comprender su significado y aplicarlo según las condiciones del problema planteado; permitiéndoles identificar, formular y resolver nuevos problemas. El planteamiento y comprobación de hipótesis para la solución de ejercicios y problemas de cálculo de integrales definidas debe permitir la obtención de nuevos conocimientos y la determinación de vías novedosas y originales para demostrar las mismas.
Al exponer y argumentar las vías de solución y los resultados de las tareas, los estudiantes deben evidenciar nuevos procedimientos, proponer algoritmos de solución alternativos y fundamentarlos, así como ofrecer nuevas vías de solución a problemas resueltos por otros. Igualmente, deben valorar autocríticamente su desempeño y el de sus compañeros.
Instrumentación y evaluación de la estrategia didáctica
La estrategia se aplica durante la preparación y el desarrollo de la asignatura Matemática Superior I en la referida carrera y el responsable es el profesor de la asignatura; aunque se sugiere participen profesores de colectivo de año y del colectivo de la disciplina.
Según la tipología de la estrategia, es necesario aclarar que estudiantes y profesores juegan un rol fundamental, pues se precisan acciones relativas a la enseñanza y al aprendizaje. En las dos primeras etapas se jerarquiza la actuación del profesor, aunque algunas de las acciones incluidas exigen la participación de los estudiantes. Las acciones de la etapa de ejecución se concretan al impartir cada clase y otras formas de organización previamente planificadas. En esta etapa, los estudiantes deben asumir una participación activa.
Por último, la evaluación de la estrategia didáctica se enfoca en el perfeccionamiento de su concepción general y de sus acciones; para ello, se realizarán grupos de discusión en los colectivos metodológicos y se sistematizarán las experiencias del profesor de la asignatura.
También, se evaluarán las transformaciones que logran los estudiantes en el nivel de desarrollo de la habilidad calcular integrales definidas. Para ello, se sugiere observar sistemáticamente su desempeño, revisar los documentos y aplicar pruebas que reflejen la solución de ejercicios y problemas relacionados con el cálculo de integrales definidas.
Como parte de los resultados, se describen los efectos que tuvo la aplicación de la estrategia didáctica luego de analizar la información recopilada de los instrumentos utilizados para evaluar el nivel de desarrollo de la habilidad calcular integrales definidas, en los estudiantes seleccionados como muestra de la investigación.
Para la medición de los indicadores, se utilizaron dos instrumentos. En la siguiente gráfica se ilustra su comportamiento, una vez triangulada la información de ambos.
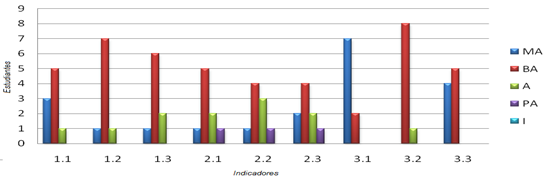
Gráf. 2- Análisis triangulado de los indicadores evaluados (elaboración propia).
A continuación, se realiza el análisis cuantitativo de cada indicador (utilizando para ello la frecuencia y la frecuencia relativa) y se argumentan, a partir de las valoraciones cualitativas que resultaron de la recopilación e interpretación de información durante el trabajo de campo con los estudiantes, reflejándose lo siguiente:
El 100 % (9) conocía la definición de integral indefinida y su significado, las propiedades y las reglas de derivación; aunque mostraron dificultades en los métodos de integración. En este sentido, los estudiantes formulaban preguntas a sus compañeros de aula y al profesor y se planteaban objetivos de aprendizaje propios.
El 88.9 % (8) domina los conocimientos asociados a las integrales indefinidas, la definición de integral definida y su significado, así como el teorema fundamental del cálculo integral; demostrando reconocer el significado de estos contenidos para su profesión.
El 77.8 % (7) conocía las aplicaciones del cálculo de integrales a la contabilidad y las finanzas; los demás no comprendían las situaciones profesionales modeladas mediante el cálculo integral. Sin embargo, se manifestaban a favor de formular o identificar problemas propios de la profesión que fuesen resueltos aplicando este contenido.
El 88.9 % (8) conocía el procedimiento para calcular integrales indefinidas y lo aplica correctamente, aunque el análisis del integrando le resultaba complejo. Los errores más frecuentes estuvieron al integrar funciones por sustitución y por partes que exigen repetir el procedimiento. Sobre este particular, los estudiantes elaboraron sus propios esquemas y, al resolver los ejercicios, intercambiaban vías de solución entre ellos.
El 88.9 % (8) aplicaba correctamente las acciones del procedimiento para calcular integrales definidas, aunque presentaron dificultad al determinar la primitiva de la función. Siempre aplicaban bien el teorema fundamental del cálculo integral y el del valor medio.
El 88.9 % (8) logró aplicar el cálculo de integrales definidas a la solución de problemas matemáticos y profesionales, lograban modelar situaciones profesionales y resolverlas e interpretar los resultados desde la perspectiva de la contabilidad, evidenciando formas de trabajo y de pensamiento matemático variadas.
El 100 % se implicó en la solución de las tareas de cálculo de integrales definidas; fueron activos al resolverlas y creían importante el estudio de estos contenidos para su profesión, así como la argumentación del proceso seguido para llegar a la solución de las tareas.
El 100 % (9) mostró satisfacción por la solución de tareas de cálculo de integrales definidas, ya que lograron una mejoría en los resultados de aprendizaje.
El 100 % (9) mantuvo una elevada disposición durante la solución de tareas de cálculo de integrales definidas, evidenciando su interés hacia el aprendizaje y considerando oportuno elaborar algunos medios o estrategias para su propio aprendizaje.
Finalmente, los autores refieren que con la aplicación de la estrategia didáctica se logró que los estudiantes utilizaran métodos y medios de aprendizaje que estimularon su participación activa y la elaboración de conocimientos, la problematización y la contextualización de las tareas profesionales; todo ello reflejado en las transformaciones que se pudieron constatar y con un efecto positivo en el nivel de desarrollo de la habilidad calcular integrales definidas al finalizar la experimentación.
DISCUSIÓN
El proceso investigativo que se describe en este artículo permite a los autores:
Significar la necesidad y pertinencia de lograr la integración coherente de las concepciones teóricas que sustentan el Proceso de Enseñanza-Aprendizaje de la Matemática con enfoque desarrollador y los lineamientos que caracterizan su enfoque metodológico en cualquier nivel educativo; y destacar lo relativo al uso de variados tipos de tareas que propicien el tránsito de los estudiantes por los diferentes niveles de asimilación, en función del desarrollo de la habilidad matemática específica que en él se trabaja.
Establecer relaciones entre los criterios teóricos de relevancia para el Proceso de Enseñanza-Aprendizaje del cálculo de integrales; es por ello que, para el desarrollo de la habilidad calcular integrales definidas, jerarquiza el uso de problemas, la comprensión conceptual, la modelación y el análisis de situaciones en vínculo con los problemas propios de la profesión.
Considerar un hallazgo novedoso, desde el punto de vista teórico, las particularidades y exigencias del aprendizaje creativo para el tratamiento del cálculo de integrales; ya que estas pueden contribuir a la formación integral de los estudiantes y, particularmente, al desarrollo de la habilidad que se estudia al implicar la utilización integrada de métodos, medios y estrategias que estimulan formas diferentes de aprendizaje.
Señalar como valor teórico del artículo el enriquecimiento de la Didáctica de la Matemática, al referirse de manera integrada a las concepciones del Proceso de Enseñanza-Aprendizaje desarrollador y sus exigencias metodológicas desde la perspectiva del aprendizaje creativo; así como en la conceptuación que se realiza de la habilidad calcular integrales definidas y el procedimiento generalizado para su desarrollo.
Describir como valor práctico del artículo la concepción general de la estrategia didáctica y sus acciones, a partir de orientar la actuación de profesores y estudiantes para el desarrollo de la habilidad matemática que se estudia; pues este exige a los estudiantes la personalización de la información, la confrontación con lo dado, la problematización de la información y la producción y generación de ideas propias.
Puntualizar que los resultados de la implementación de la estrategia didáctica reafirman la posibilidad de socializarla y, a su vez, perfeccionarla, ya que aunque se lograron niveles superiores de desarrollo de la habilidad calcular integrales definidas en los estudiantes con que se trabajó se identifican elementos que pueden ser mejorados para lograr un mayor alcance en esta y otras carreras universitarias.
REFERENCIAS BIBLIOGRÁFICAS
Álvarez Pérez, M., Almeida Carazo, B. y Villegas Jiménez, E. V. (2014). El proceso de enseñanza-aprendizaje de la asignatura matemática documentos metodológicos. La Habana: Pueblo y Educación.
Ballester Pedroso, S., García La Rosa, J. E., Almeida Carazo, B., Álvarez Pérez, M., Rodríguez Ortiz, M., González Noguera, R. A., Villegas Jiménez, E. V., Fonseca González, A. L. y Puig Reyes, N. (2018). Didáctica de la Matemática (Tomo 1). La Habana: Pueblo y Educación.
Ferrer Vicente, M. y Rebollar Morote, A. (1995). Cómo dirigir el proceso de formación de habilidades matemáticas [Curso]. Curso impartido en el Evento Internacional Pedagogía 1995. La Habana: Cuba.
Fonseca Castro, J. L., y Alfaro Carvajal, C. R. (2018). El cálculo diferencial e integral en una variable en la formación inicial de docentes de matemática en Costa Rica. Revista Educación, 42(2), 1-22. https://revistas.ucr.ac.cr/index.php/educacion/article/view/25844
Granera Rugama, J. A. (2019). La integral definida como el área bajo una curva en un entorno computacional. Revista Científica de FAREM-Estelí, 8(30). https://dialnet.unirioja.es/descarga/articulo/7304343.pdf
Martínez Castellini, A. (2020). Uso de métodos problémicos en el proceso de enseñanza aprendizaje de la matemática: metodología para calcular integrales indefinidas. Revista Universidad y Sociedad, 12(5), 445-453. https://rus.ucf.edu.cu/index.php/rus/article/view/1731
Mitjáns Martínez, A. (2013). Aprendizaje creativo: desafíos para la práctica pedagógica. Revista CS, 11. https://doi.org/10.18046/recs.i11.1574
Rodríguez del Castillo, M. A. y Rodríguez Palacios, A. (2011). La estrategia como resultado científico de la investigación educativa. En N. De Armas Ramírez y A. Valle Lima (Eds.), Resultados científicos en la investigación educativa. (pp. 20-51). Pueblo y Educación: Cuba.
Rojas Taño, A. y Rodríguez Sosa, J. B. (2021). La significatividad del aprendizaje del cálculo diferencial e integral. VARONA. Revista Científico Metodológica, 72(enero-junio), 11-15. http://revistas.ucpejv.edu.cu/index.php/rVar/article/download/1135/1513
Sánchez Companioni, W., Pérez González, A. y Remedios González, J. M. (2022). El aprendizaje creativo: una alternativa para el proceso de enseñanza y aprendizaje de la Matemática. Pedagogía y Sociedad, 25 (63), 312-331. http://revistas.uniss.edu.cu/index.php/pedagogia-y-sociedad/article/view/1278
Suárez Rincón, M. L. (2018). Estrategias pedagógicas para la enseñanza de las matemáticas en Administración: Estudios y experiencias. Revista Electrónica Interuniversitaria de Formación del Profesorado, 21(2), 79-89. DOI: https://doi.org/10.6018/reifop.21.2.323261
Rodríguez Saltos, E. R., Vallejo Loor, B. M., Yenchong Meza, W. E., y Ponce Solórzano, M. J. (2020). Importancia de la psicopedagogía y el aprendizaje creativo. Dominio de las Ciencias, 6(3), 564-581. http://dx.doi.org/10.23857/dc.v6i3.1300
Villena Muñoz, M., y Rivas Maldonado, N. (2019). Impacto del uso de la tecnología en el proceso de enseñanza- aprendizaje del cálculo integral. Revista Conrado, 15(68), 297-307. https://conrado.ucf.edu.cu/index.php/conrado/article/view/1028Villenas
Conflicto de intereses:
Los autores declaran no tener conflictos de intereses.
Contribución de los autores:
Los autores participaron en el diseño y redacción del trabajo, y análisis de los documentos.
![]()
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial 4.0 Internacional
Copyright (c) Wilfredo Sánchez Companioni, Andel Pérez González & Juana María Remedios González.