

Revista Mendive, enero-marzo 2017; 15(1):6-19
El aprendizaje por proyectos en el tratamiento de la estadística durante la formación pregraduada de profesores de Matemática
Learning by Projects in Teaching Statistics during Initial Formation of Mathematics Teachers
Carlos Luis Fernández Peña1, Leonel Reinoso Acosta2
1Licenciado en Educación. Especialidad Matemática. Máster en Ciencias de la
Educación. Doctor en Ciencias Pedagógicas. Universidad de Pinar del Río «Hermanos Saíz Montes
de Oca». Correo electrónico: carlosl.fernandez@upr.edu.cu
2Licenciado en Educación, Especialidad Matemática. Máster en Ciencias de la
Educación. Profesor de Probabilidades y Estadística en el departamento de
Matemática-Física. Universidad de Pinar del Río «Hermanos Saíz Montes de
Oca». Correo electrónico: leonel.reinoso@upr.edu.cu
Recibido: 19 de septiembre de 2016.
Aprobado: 15 de diciembre de 2016.
RESUMEN
Las tendencias actuales, relacionadas con el tratamiento de la Estadística en la formación pre graduada de profesores de Matemática, apegados al planteamiento de ejercicios y problemas descontextualizados, carentes del enfoque profesional y alejados de la actividad investigativa, no responden a la necesidad de formar un profesor capaz de dominar estos contenidos como parte de lo que enseña y como recurso investigativo. Esta situación plantea la necesidad de realizar innovaciones didácticas que superen tales limitaciones. El presente artículo da cuenta de la solución planteada a la problemática descrita en la Universidad» Hermanos Saíz Montes de Oca» de Pinar del Río. La solución se basa en el aprendizaje por proyectos, sustentado en tres pilares: la integración, la exploración y la problematización. Bajo estas ideas se logró que el futuro profesional se enfocara en la solución de un problema de la profesión con datos propuestos por ellos, los que una vez capturados sirvieron de soporte para el desarrollo de todas las actividades docentes (conferencias, clases prácticas, seminarios). En la búsqueda y el procesamiento de la información empírica, se combinaron métodos cualitativos y cuantitativos, mientras que el tratamiento de la información teórica se hizo básicamente a partir de los métodos histórico -lógico y la modelación. Su contextualización tuvo lugar en cuarto y quinto años de la cohorte que se graduó en el curso 2015-2016, con resultados alentadores en términos de significación del contenido, así como independencia, flexibilidad, consecutividad, profundidad y comprensión de los procesos mentales durante la solución de los problemas.
Palabras clave: Aprendizaje, proyecto, contenidos estadísticos, problematización, integración, exploración.
ABSTRACT
Current trends related to teaching statistics for mathematics teachers in formation, who follow a series of exercises and problems out of context, lack of any kind of professional approach and too far from research activities, do not respond to the need of forming a teacher able to master the contents as a part of the whole thing they teach, and a resource to investigate. This situation tells us the need of making teaching innovations to be over such insufficiency. This article reveals the solution to the problem described above at the Pinar del Rio University «Hermanos Saiz Montes de Oca» The solution is based on three stone posts of learning by projects: integration, exploration and problematization. Under these ideas we guaranteed an approach based on solving professional problems using data they proposed which also were useful in supporting all teaching activities such as lectures, practical lessons, and seminaries. In seeking and processing information, quantitative and qualitative methods were used; meanwhile, all the theoretical info was treated using methods like historical logical and modelation. All that was brought to context on fourth and fifth years of 2016 class with very encourage outcomes in terms of independence significance of contents, flexibility, continuity, profundity and comprehension of mental process during the activity of solving problems.
Key words: learning; projects; statistics contents; problematization; integration; exploration.
INTRODUCCIÓN
Weaver, W. (2003) reveló que, desde épocas tan tempranas como el siglo XIX, H. G. Wells, autor de The War of the Worlds y The Time Machine, decía que «el pensamiento estadístico sería algún día tan necesario para el buen ciudadano, como la habilidad para leer y escribir» (p.1). Este planteamiento ha trascendido los tiempos y cobra hoy, en la sociedad de la información y las comunicaciones, un gran significado.
¿Es esta máxima atribuible al profesor de Matemática cubano de la actualidad?
No cabe duda que la respuesta a esta interrogante es positiva, en primer lugar porque, como cualquier ciudadano, necesita tener una imagen equilibrada de la realidad en la que hay una fuerte presencia de fenómenos aleatorios; en ese sentido, debe ser capaz de comprender y poner en práctica la Estadística, no solo como un sistema de conceptos y técnicas, sino, y sobre todo, como una forma de razonar en situaciones de incertidumbre para hacer inferencias y guiar la toma de decisiones a partir de los datos.
Por otro lado, también la Estadística como contenido de enseñanza en la formación de profesores, como señalara Begg (1997), es un vehículo ideal para alcanzar las capacidades de comunicación, tratamiento de la información, resolución de problemas, uso de ordenadores, trabajo cooperativo y en grupo.
En segundo lugar, el desempeño de los profesores de Matemática depende, en gran medida, del dominio que tengan de los contenidos estadísticos para enseñarlos y usarlos como recursos para investigar sobre su propio trabajo.
Pero es necesario reconocer que, aunque la importancia de esta ciencia es reconocida por no poco estudiosos del tema en el mundo, en el currículo de la formación de profesores de Matemática en Cuba estuvo ausente por más de 20 años, lo que ha traído retraso en la evolución de las estrategias de su enseñanza en este nivel. La actualización de estas estrategias debe ser enfrentada desde el campo de innovación, desarrollo e investigación.
Esta es la razón por la que la disciplina de Probabilidades y Estadística en la formación de profesores de Matemática, en la Universidad «Hermanos Saíz Montes Oca» se planteó como problema ¿Cuál es la estrategia didáctica adecuada que contribuye a mejorar el dominio, la comprensión, la valoración, el uso y las actitudes para el proceso de enseñanza-aprendizaje de la Estadística, en la formación de profesores de Matemática?
La estrategia metodológica surgida, como respuesta a este problema, tiene como pilares básicos la problematización, la exploración y la integración a partir del trabajo con proyectos estadísticos.
Los resultados esperados con la implementación de la estrategia están referidos a la elevación de los niveles de significación de la Estadística para resolver problemas, la independencia en el proceso de solución de problemas estadísticos, flexibilidad en el proceso de compresión e instrumentación de las soluciones, la consecutividad del proceso de solución, la profundidad de las ideas en las soluciones planteadas y la comprensión adecuada de los procesos mentales implicados en la solución.
MATERIAL Y MÉTODOS
La muestra utilizada en el proceso investigativo que se da cuenta en este artículo fue seleccionada teniendo en cuenta que la disciplina Probabilidades y Estadística está presente en el cuarto y el quinto años de la carrera, razón por la cual es necesario tomar una cohorte completa para desarrollar la etapa experimental. En este caso, se utilizó la cohorte graduada en el curso 2015-2016.
En la búsqueda y el procesamiento de la información teórica. se usaron básicamente los métodos Histórico-Lógico para sistematizar el proceso evolutivo de las formas de enseñanza de la estadística en la formación de profesores de Matemática y la modelación para lograr la aproximación más exacta posible a los elementos fundamentales del proceso de enseñanza-aprendizaje de estos contenidos y su funcionamiento en el contexto descrito.
La puesta en práctica de la estrategia didáctica se hizo mediante un preexperimento con la modalidad de aplicación de las acciones-evaluación final.
Dada la naturaleza del contenido estadístico en el seguimiento a los resultados alcanzados, se utilizaron un conjunto de indicadores que fueron evaluados mediante la escala: Alto (A), Medio (M) y Bajo (B).
Para la captura de la información, se utilizó una guía de observación acompañada de un interrogatorio con el que se emplazaba al alumno para que explicara el proceso seguido. Con el primer método se le dio seguimiento a la actividad del alumno y con el segundo se logró identificar las razones que lo movieron a realizar cada una las acciones.
El procesamiento de la información se hizo a partir de un análisis de las frecuencias expresadas como por cientos, la prueba Kolmogorv-Smirnov de bondad y ajuste para la muestra.
RESULTADOS
El proceso investigativo permitió alcanzar como resultado, la sistematización de los antecedentes en el objeto en estudio, lo que posibilitó la elaboración de la estrategia didáctica que se propone.
Elementos esenciales de la estrategia didáctica propuesta
I- Utilizar el proyecto estadístico integrador durante las 68 hora lectivas que abarcan las asignaturas Probabilidades y Estadística I y II de la disciplina «Probabilidades y Estadística».
II- Utilizar la variante de aprendizaje por proyectos (APP) en el cuarto año de la carrera, es decir, el estudiante construye su aprendizaje en la misma medida en que va dando solución a las tareas del proyecto. En este caso, una vez elaborado el proyecto de conjunto con los estudiantes, este sirvió de guía al curso. El desarrollo de cada actividad motivó la necesidad de enfrentar un tema del programa, lo que fue hecho, en la mayoría de los casos, de forma independiente por el estudiante o tratado en clases a solicitud de estos.
El objetivo en este caso fue: resolver un problema propio de la investigación educativa a partir del uso de la estadística descriptiva, de manera que permita a cada estudiante, a la vez que desarrolla la misma, conformar su propio aprendizaje sobre estos contenidos y su uso en este campo.
III- Utilizar la variante de aprendizaje orientado a proyecto (AOP) en quinto año de la carrera, donde la esencia es poner en práctica lo aprendido en las clases de la asignatura Probabilidades y Estadística II. La segunda parte del proyecto tuvo como objetivo lograr que los estudiantes fueran capaces de: integrar los conocimientos adquiridos sobre las probabilidades y la estadística inferencial a la solución de problemas de la investigación educativa.
IV- Utilizar, por este orden, los cuatro tipos de situaciones didácticas siguientes en el desarrollo de las actividades para enfrentar el contenido:
Dada la escasa experiencia de los estudiantes en el trabajo por proyectos, en la estructuración del mismo se utilizó una guía (ver anexos 1 y 2) que permitió dar la mayor cantidad de informaciones de una vez y que además le sirviera de material de consulta durante el período de trabajo.
Resultados de la puesta en práctica de la propuesta.
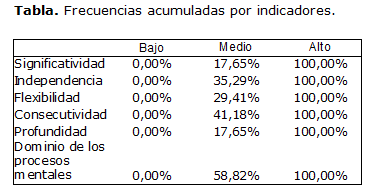
Los resultados de la prueba Kolmogorov-Smirnov para una población con un nivel de significación de 0,05 mostró para un estadígrafo D=0,67 y una región crítica D0,95(17) =0,318 para todos los indicadores.
DISCUSIÓN
Análisis de las tendencias generales en la enseñanza de la estadística
Desde el punto vista de las tendencias de enseñanza de la Estadística, hay que reconocer los señalamientos de Fernández (2009) en relación con los estudios realizados por (Behar, 2001)en relación con la existencia de tres concepciones fundamentales que distinguen este proceso: la concepción tradicional, la basada en las probabilidades y el Análisis Exploratorio de Datos (AED).
La concepción tradicional concibe el contenido como entes matemáticos abstractos, basados en el planteamiento de ejercicios y problemas, generalmente descontextualizados. En este caso, el objetivo preferente es la actividad matemática abstracta y no la actividad estadística propiamente dicha, pues las aplicaciones no son realmente importantes y los alumnos finalizan los cursos sin adquirir una competencia real para llevar a cabo una investigación estadística acorde con las aspiraciones del proceso de formación.
Debido al papel jugado por las probabilidades, la Estadística ha dado al traste con una concepción basada en ellas, Behar (2001) plantea que: «Este enfoque ha sido discutido seriamente. Muchos artículos recientes plantean que es posible entender los conceptos básicos de la estadística para su adecuada aplicación, con pocos conocimientos relativamente formales de probabilidad, haciendo más énfasis en la intuición y en la simulación y dando los preliminares de la inferencia con base en el análisis de datos más que en modelos matemáticos de probabilidad» (p.194)
Aquí se recorre primeramente un largo camino en el mundo de las probabilidades, invirtiendo buena parte del tiempo en temáticas como la combinatoria, dando un tratamiento más o menos formal a temas clásicos de la teoría de la probabilidad que contribuyen, de ese modo, a la atomización del currículum y a situar el centro de la atención en contenidos complejos como los de la Combinatoria y las Probabilidades y no en la Estadística.
Es importante señalar que es necesario que el alumno tenga cierta comprensión de los fundamentos probabilísticos de la Estadística. En ese sentido, es necesaria la comprensión de la relación entre conceptos como fenómenos aleatorios y deterministas, con los sucesos imposibles, posibles, seguros, probables, así como de conceptos tales como: espacio muestral y muestra, sucesos equiprobables y la asignación de probabilidades a un suceso sencillo de la vida.
Como respuesta a las deficiencias de las concepciones anteriores es introducido por (Tukey, 1962; 1970) el Análisis Exploratorio de Dato (AED). Esta es la forma más reciente de concebir el proceso de enseñanza-aprendizaje de los contenidos estadísticos, la cual se ha extendido como filosofía de aplicación de la estadística, debido a la disponibilidad de ordenadores y software estadísticos con posibilidades de representación gráfica y tratamiento de conjuntos de datos variados. Esta concepción se manifiesta en el enfoque interdisciplinario para la enseñanza de la Estadística propuesta por (Mattana, 2006).
La filosofía del Análisis Exploratorio de Datos se aleja de los cálculos para acercarse a la investigación, a la búsqueda de conclusiones y al establecimiento de relaciones entre datos y entre variables. El Análisis Exploratorio de Datos utiliza las informaciones publicadas en: redes computacionales o computadoras aisladas, anuarios estadísticos, la prensa, o en los datos recogidos por los alumnos (mediciones, encuestas, etc.).
Manifestaciones de estas tendencias en el diseño curricular de la formación de profesores de Matemática en Cuba
Los estudios realizados revelaron que los planes A y B para la formación de profesores de Matemática en Cuba tenían incluidos estos contenidos; pero su tratamiento se llevaba a cabo desde una perspectiva puramente matemática, desvinculada de la resolución de problemas y la actividad investigativa. El caso del plan C fue más crítico porque dichos contenidos fueron desapareciendo paulatinamente en la medida en que sufrió reajustes y trasformaciones.
Ya en las distintas versiones del plan D, la enseñanza de la estadística se ha incorporado con fuerza, ocupando, al menos en teoría, el lugar que le corresponde como instrumento de la investigación educativa y como recurso para comprender el mundo actual cada vez más interconectado y dependiente de la disponibilidad y compresión de la información.
Una tendencia en la formación de profesores, en la actualidad, concibe la enseñanza de la estadística como patrimonio de los profesores de esta disciplina, o bien de los investigadores, siempre y cuando llegue el momento de procesar los datos que genera su trabajo. Esta percepción es errónea, puesto que la educación estadística ha surgido desde la misma estadística como una necesidad social que ayuda a tomar decisiones en distintos contextos.
Para Ottaviani, M. G. (1998) la escuela debe responder a «... la necesidad de difusión de la estadística, no solo como una técnica para tratar los datos cuantitativos, sino como una cultura, en términos de capacidad de comprender la abstracción lógica que hace posible el estudio cuantitativo de los fenómenos colectivos». (p.20)
En relación con las concepciones erróneas sobre la estadística en la enseñanza es necesario tener en cuenta lo señalado por Batanero (2003) en el sentido de que « puesto que las investigaciones psicológicas sugieren que las intuiciones erróneas no se corrigen con una mera enseñanza expositiva, ni tampoco con la ejercitación en el cálculo o en la resolución de problemas rutinarios, será necesario que la introducción de la estadística, en las escuelas, vaya acompañada de una renovación de los métodos de enseñanza para que llegue a ser realmente efectiva» (p.2).
La integración, la exploración y la problematización como pilares de la enseñanza de la Estadística en la formación de profesores de Matemática
Contrario a la tendencia tradicional de la enseñanza de la Estadística, se busca con este enfoque que el estudiante se vea reflejado en lo que aprende, como ciudadano y como futuro profesional, donde los contenidos estadísticos, más que una simple materia de estudio, sean herramientas para tomar decisiones.
Partiendo de lo señalado por Zurbano, E., Corral, C. Y Díaz, I. (2003) « (...) los números vienen determinados por intereses e intenciones, por lo que no son tan solo medios para interpretar y comprender una situación...» (p.1), se busca insertar al estudiante en el ciclo búsqueda-procesamiento-comunicación, propio de la actividad estadística, desde contextos afines donde afloren los motivos que generan la necesidad de caracterizar numéricamente una situación real, hacer inferencias sobre ella y guiar la toma de decisiones.
La enseñanza de los contenidos estadísticos debe tener presente la utilización de problemas contextualizados dentro y fuera del aula, que estimulen, por una parte, el componente afectivo mediante la motivación intrínseca hacia el estudio de la estadística y, por la otra, indique las líneas principales del proceso de transformación de la forma externa material de la actividad estadística en la forma interna, psíquica; en ese sentido la consideración del aspecto afectivo-motivacional debe ser esencialmente profesional, aunque no descarta variantes como el vínculo con otras áreas del saber como la Física o las ciencias sociales.
Por otra parte, lo fundamental, según Labarrere (2000) es que el planteamiento de las acciones de aprendizaje tenga en cuenta que el estudiante, más que solucionar independientemente el problema que ayer resolvía con ayuda del otro, debe ser capaz de orquestar acciones tendentes al desarrollo propio o de su grupo.
Esto implica que la acción en la Zona de Desarrollo Próximo durante la solución de los problemas debe propiciar, ante todo, la formación de la autoayuda, el autoandamiaje, la autoasistencia, para lo cual es necesario que los procesos formativos traigan a un primer plano la transferencia metacognitiva como intento consciente y explícito de que al estudiante se le hagan claras las intencionalidades, para que apropiándoselas y desarrollando las suyas propias, pueda poner su desarrollo al servicio de mejores y más amplios aprendizajes ulteriores y así lanzar estos en pos de nuevos niveles de desarrollo.
También es necesario poner un acento especial a la comunicación, el carácter social de la actividad y el lenguaje. La comunicación se considera como una forma de interacción sujeto-sujeto(s), la cual transcurre a través de un intercambio cognoscitivo-afectivo, tomando en cuenta los objetivos individuales y colectivos a los que se dirige sobre la base de las motivaciones.
Para el logro de lo anterior, se busca hacer consciente al estudiante de por qué las acciones están directamente orientadas hacia los contenidos estadísticos (como recurso para lo investigativo, como contenido de enseñanza y como recurso para comprender los fenómenos de la realidad); para ello debe lograrse que la actividad estadística ocupe un lugar dentro del objetivo de la acción interna o externa. Las actividades deben orientarse de modo tal que el estudiante tome conciencia del papel de la Estadística en su formación y en la solución de problemas de la vida.
Lo integrador se presenta a partir de los aportes de (Fiallo, F. 1999, 2001; Perera, F. 2002, 2006; Álvarez, M.2002, 2003; Mattana, G. 2006), como una alternativa para el planteamiento de problemas que permitan el enriquecimiento mutuo en un plano de igualdad de las disciplinas, lo que facilitaría la contextualización del proceso de enseñanza-aprendizaje de los contenidos estadísticos en la formación de profesores de matemática.
Lo integrador es parte de la sistematización para la aplicación contextualizada de los contenidos en la solución de problemas con marcado corte investigativo e indagatorio sobre actividades propias de la profesión.
Todo ello es parte de un enfoque interdisciplinario para la enseñanza de la estadística, tomando en cuentaque lo planteado por Mattana (2006) en relación con que «…los conceptos estadísticos, a pesar de su abstracción, expresan un resultado del mundo real, muchas veces de la aplicación en otras ciencias y en innumerables aspectos prácticos de la vida diaria: en la industria, en el comercio, en la tecnología, etc., por lo que la enseñanza y el aprendizaje de estos contenidos en la escuela deben hacerse desde posiciones interdisciplinarias». (p.23).
La exploración se basa en el establecimiento de una estrecha relación entre la teoría y la práctica, donde se estimule la indagación, la búsqueda de datos, usando diversas fuentes, el trabajo colectivo, el debate, la reflexión, la búsqueda de un conocimiento integrador e interdisciplinario, la interacción de alumnos, profesores, familia y comunidad.
Para garantizar lo exploratorio, se parte de los métodos de indagación critico-creativos, planteados por (González, M. 2004), pues a través de ellos se amplían las capacidades de los alumnos para explorar, para hacer preguntas, investigar y llegar a conclusiones.
Esta autora refiere dos variantes para estos métodos: la A, que representa el nivel básico y precedente, a diferencia de la B, que encausa la indagación en torno a los objetivos, tipos y funciones del aprendizaje; esta última modalidad del método requiere de mayor protagonismo por los estudiantes y mayor dominio de la lógica de la disciplina.
En correspondencia con los planteamientos de (Batanero, C.1999 y Mattana, G. 2006) en relación con el enfoque interdisciplinario, es importante entrar a considerar la enseñanza problémica para que los estudiantes se sitúen sistemáticamente ante problemas, cuya resolución debe realizarse con su activa participación, y en la que el objetivo no es solo la obtención del resultado, sino, además, su capacitación para la resolución independiente de problemas en general.
Para un enfoque problémico de la enseñanza, se toman en cuenta los principios en que se sustenta la enseñanza problémica que formuló Martínez (1999) que son: «la relación del contenido de la ciencia con su método de enseñanza, el establecimiento de la unidad de la lógica de la ciencia con la lógica del proceso docente y la consideración del nivel de desarrollo de las habilidades de los estudiantes». (Pp.13-29).
Buscando un plano más específico se tuvo en cuenta también el papel de los problemas en la enseñanza-aprendizaje de la estadística; en este aspecto, se tomarán los significados atribuidos por Villanova (2005), es decir: resolver problemas como contexto, resolver problemas como habilidad y resolver problemas como un modo de desarrollar la estadística.
Con respecto a estas formas de usar los problemas, hay que señalar que para su uso en la formación de profesores es necesario un equilibrio entre ellas, pues las características propias de este contenido dependen de su necesaria contextualización y, a la vez, trata de la asimilación de un complejo sistema de acciones asociadas a un tipo específico de actividad, por lo que no se puede separar de las habilidades; finalmente, la Estadística es una herramienta investigativa y debe ser aprendida como tal; de ahí el valor del tercer significado en esta investigación.
Finalmente, para la creación de situaciones didácticas que recojan los presupuestos referidos anteriormente, tal y como señalara Brousseau (1986), hay que tener en cuenta el grupo de estudiantes y el profesor, así como el medio didáctico que incluye los problemas, materiales e instrumentos que el profesor proporciona a los estudiantes, con el fin específico de ayudarlos a reconstruir un cierto conocimiento.
Desde esa perspectiva, se estimuló la filosofía del trabajo con proyectos que permitan dotar de un significado más completo a los conceptos estadísticos, a partir de situaciones variadas conectadas con otras áreas curriculares o con los intereses de los estudiantes.
El trabajo por proyectos es un método propio de los enfoques interdisciplinarios y, consecuentemente, del Análisis Exploratorio de Datos, donde coexisten de manera armónica los componentes de la tríada integración-exploración-problematización.
Elementos conceptuales de la enseñanza y el aprendizaje por proyectos
El surgimiento de este método se remonta al Movimiento Escuela Nueva como una forma de utilizar los intereses de los estudiantes para aumentar su rendimiento; de ahí que este deberá pasar de un mero receptor de experiencias ajenas de aprendizaje a autor de las suyas propias. En este sentido, surgen así los métodos centrados en los estudiantes, o sea, los métodos activos.
Este método surge de la mano del norteamericano William Heard Kilpatrick como forma de dar prioridad a la actividad práctica de los estudiantes. Kilpatrick clasificó los proyectos en cuatro grupos: proyectos para incorporar alguna idea o habilidad, proyectos para experimentar algo nuevo, proyectos para poner orden en alguna dificultad intelectual y proyectos para obtener una información o realizar algunas prácticas.
Para Fiallo (2005), los proyectos en educación «…son modos de organizar el proceso de enseñanza-aprendizaje abordando el estudio de una situación problemática para los alumnos, que favorece la construcción de respuestas a las interrogantes formuladas por estos» (p.72).
En este modo de concebir el enseñar y aprender, se genera una situación dinámica en donde todos los participantes se involucran (profesor-estudiante), a partir de la conciliación de sus intereses en relación con la compresión, la explicación y la valoración de la realidad.
Así, el aprender le permite al estudiante utilizar sus propios razonamientos y procedimientos, lo que implica que cometerá errores necesarios en la búsqueda de razonamientos correctos al observar, investigar, realizar trabajos, construir esquemas, formular preguntas y resolver situaciones problemáticas.
Trabajar en un proyecto supone que los contenidos programáticos sean instrumentos para promover el desarrollo de habilidades en torno a un interés, nacido propiamente de la voluntad del estudiante, en dos direcciones: una de interrogación y otra de resolución; este nexo entre interés y voluntad genera acciones concretas, las que significan tomar decisiones y las de generar preguntas.
Este proceso generador de preguntas y respuestas encaja perfectamente como parte del sistema didáctico apropiado para el aprendizaje de la estadística; este es un recurso de innegable valor para el desarrollo de procesos exploratorios que permiten la producción, el procesamiento y la comunicación de datos. Ello significa que las preguntas, las respuestas y las acciones posteriores con las informaciones procesadas son creación de los participantes.
Con el trabajo por proyectos, al encarar los pasos del método estadístico, el estudiante tiene la libertad de seguir una secuencia creada por él, siendo esta su riqueza principal, pues la flexibilidad que existe entre las estrategias y procedimientos que definen a cada uno de los momentos del proceso del método y, sobre todo, la flexibilidad en lo que se refiere a los tiempos de cada una de las fases, permite que el aprendizaje se parezca más a la vida.
Estas características del método hacen plausible su uso en la enseñanza de la estadística en la formación de profesores de Matemática; dan fe de ello los aportes de Batanero (1999), Mattana (2006), específicamente en la formación de maestros y de Fernández (2009) en el trabajo con estudiantes de Secundaria.
Como señalara Batanero (2003), este tipo de metodología es muy apropiada en el contexto universitario. En investigaciones como la de Tauber (2001) sobre la enseñanza de la distribución normal con un enfoque intuitivo, basado en los proyectos de análisis de datos y el uso de ordenadores, se logró que los alumnos participantes, finalmente, alcanzaran una comprensión intuitiva de gran parte de los elementos de significado de la distribución normal, incluso aquellos que estudiaban estadística por primera vez.
El aprendizaje, que los estudiantes planean, implementan y evalúan proyectos que tienen aplicación en el mundo real más allá del aula de clase, es recogido por la literatura como Aprendizaje Basado en Proyectos (ABP).
Las dos direcciones más usuales del aprendizaje por proyectos se distinguen por sus finalidades más internas, es decir, cuando se aprende acerca de algo, reconocido como aprendizaje basado a proyectos (ABP) y cuando se aprende haciendo algo, aprendizaje orientado a proyectos (AOP). Las diferencias entre estas dos modalidades, aunque casi imperceptibles, se dan porque en la primera el estudiante aprende en la misma mediada en que desarrolla el proyecto, mientras que en la segunda aplica lo aprendido en clases al desarrollo de un proyecto, no obstante, las dos juegan el papel de hilo conductor del proceso de enseñanza, una vez elaborado el proyecto.
Con el aprendizaje por proyectos, en el caso particular de los contenidos estadísticos en la formación de profesores de Matemática, se busca contribuir a la apropiación de procedimientos y estrategias que les permitan producir, crear, reflexionar y valorar estos conocimientos a partir de intereses reales relacionados con la profesión.
Con el uso del aprendizaje por proyectos se espera obtener, como resultado, la formación de profesionales con habilidades para resolver problemas en contextos estadísticos, de manera reflexiva y crítica, además de apropiarse de experiencias que le garanticen una interacción inteligente en contextos cambiantes y complejos de su profesión.
Esta forma de organizar el aprendizaje favorece el desarrollo de una actitud investigativa y constructiva del conocimiento, respondiendo a una motivación intrínseca que va más allá del contenido propiamente dicho y penetra en la profesión.
Los enfoques señalados (APP y AOP), permiten trabajar, desde y/o para el proyecto, en la determinación, conjuntamente con el profesor, el qué, cómo y para qué de los aprendizajes de acuerdo con sus saberes y potencialidades; así como su aplicabilidad en contextos similares donde fueron alcanzados.
Con el uso del enfoque APP se busca desarrollar procesos indagatorios tomando el contexto profesional como plataforma para aprender estadística, lo que significa explorar el comportamiento de los ámbitos sociales, culturales, políticos, educativos, geográficos, históricos y económicos que tienen que ver con el desarrollo del Proceso Docente Educativo donde realizan su actividad profesional.
El aprendizaje orientado a proyectos (AOP) pretende que los estudiantes asuman una mayor responsabilidad de su propio aprendizaje, así como aplicar, en proyectos reales, las habilidades y conocimientos adquiridos en su formación. Su intención es encaminar a los estudiantes a situaciones que los lleven a rescatar, comprender y aplicar lo que aprenden como una herramienta para resolver problemas y realizar tareas, es decir, poner a los contenidos estadísticos en función de la toma de decisiones propias de la profesión.
La adecuación del método de proyectos para lograr la relación integración-exploración-problematización en la formación de profesores de matemática tiene en cuenta los planteamientos de Batanero, Estepa y Godino (1992), Batanero (1999), Behar (2003), Terán (2005), Mattana (2006) y Fernández (2009) para la creación de situaciones de aprendizaje, en las que se concretan los enfoques interdisciplinarios, defendidos para el caso específico de la enseñanza de los contenidos estadísticos.
Se definen, entonces, los Proyectos Estadísticos Integradores como conjuntos de tareas articuladas a partir de un problema principal, cuyo proceso de solución, por la vía estadística, permite organizar las actividades de los alumnos por un período de tiempo determinado para garantizar el aprendizaje de los contenidos relacionados con la Estadística.
La posición de estos proyectos estadísticos integradores dentro del proceso de enseñanza-aprendizaje de los contenidos estadísticos determina la manera en que se dan las relaciones del método con los restantes componentes; así como las relaciones entre los componentes personales del proceso.
Los proyectos estadísticos integradores se estructuran a partir de:
El problema principal se deriva de una situación problémica enmarcada en la lógica de la actividad estadística: problema-búsqueda-procesamiento-comunicación de resultados.
Los problemas parciales representan, cada uno, acciones de ciclo: búsqueda- procesamiento-comunicación de resultados.
Las tareas complementarias deben ser de fijación del contenido estadístico y de apoyo a la solución del problema principal.
El cronograma de solución garantiza el desarrollo de motivaciones para la actividad a realizar; el planteamiento de metas para perfeccionar el trabajo independiente que realiza; la formación de valores relativos al trabajo independiente y la reflexión sobre su proceso de aprendizaje para perfeccionarlo.
Los análisis realizados hasta este punto dan cuenta de que, en Cuba, la enseñanza de la Estadística, en los distintos planes de estudio de la formación de profesores de Matemática, ha estado marcada por una perspectiva puramente matemática, carente de un enfoque profesional, desvinculado de la resolución de problemas y la actividad investigativa.
Debido a las influencias negativas que la presencia de esta tendencia ha tenido en los resultados de la formación de profesores de Matemática, se ha diseñado una estrategia didáctica para el proceso de enseñanza-aprendizaje de la Estadística que debe prepararlo para el cumplimiento de sus funciones como docentes, tomando como base el aprendizaje por proyectos, tanto en la modalidad de Aprendizaje Basada en Proyecto como la Orientada a Proyectos, es decir, atender a la construcción y aplicación del conocimiento en situaciones reales, para lo cual es vital el enfoque integrador de la Estadística con otras disciplinas, el planteamiento de actividades que fomente la exploración e investigación desde la profesión y la problematización de las tareas.
Análisis de los resultados empíricos por indicadores
Con el desarrollo de las actividades propuestas, se lograron resultados alentadores en relación con el nivel de significación de la Estadística para resolver problemas de la profesión; el 82,3% (14) de los 17 alumnos del grupo pudo identificar la solución del problema general propuesto como un proceso estadístico con abundantes detalles, mientras que el resto propuso soluciones donde se pudieron identificar solo algunos aspectos de la Estadística.
Se mejoró paulatinamente la independencia de los estudiantes; en este aspecto se logró que el 64,7% (11) pudiera realizar el proceso adecuadamente en situaciones nuevas con ideas novedosas, sin la ayuda externa; los restantes solo llegaron a realizar el proceso adecuadamente con ideas nuevas, sin ayuda del profesor, solo en situaciones conocidas.
Con relación a la flexibilidad del pensamiento (si ante una situación nueva con variaciones con respecto a las conocidas es capaz de adecuarse al nuevo contexto independientemente) lograron llegar a hacerlo con éxito 70,5% (12) de los alumnos, mientras que el resto necesitó la ayuda del profesor.
El análisis de en qué medida los estudiantes realizan el proceso de solución, siguiendo un orden que se corresponda con la lógica de la actividad estadística de forma independiente, demostró que solo pudieron llegar a resultados óptimos el 58,8% (10), el resto logró ese nivel de consecutividad solo con ayuda externa.
El análisis de las respuestas, dadas en distintos momentos del proceso en relación con la profundidad con que lograban hacerlo, mostró que el 82,3% (14) llegó a realizar el proceso correctamente teniendo en cuenta los aspectos esenciales necesarios para dar una respuesta completa.
En relación con las comprobaciones realizadas para verificar si las respuestas eran el resultado de procesos mentales conscientes, se encontró que prevaleció cierta tendencia a la ejecución en el 41,1 % (7) de los estudiantes, aunque el resto pudo explicar con abundantes detalles el proceso de solución.
La aplicación de la prueba Kolmogorv-Sminov para una población, con un nivel de significación de 0,05, permitió rechazar la hipótesis de que no existirían diferencias significativas en relación con la distribución de los alumnos en las distintas categorías de la escala con que fueron evaluados; lo que permite afirmar, con un nivel de confianza del 95%, que las significativas acumulaciones de la frecuencia en la categoría de alto de la escala, en cada indicador, no pueden ser atribuidas a la casualidad.
Por lo antes expuesto se llega a la conclusión de que existe una estrecha relación entre la aplicación de la estrategia didáctica y los resultados mostrados en la cohorte que fue aplicada en relación con el aprendizaje de la Estadística.
ANEXO 1. Guía para el desarrollo del proyecto en la asignatura Probabilidades y Estadística I (cuarto año de la carrera).
PRINCIPALES ACTIVIDADES
Actividad 1: Haga un análisis de la evolución de la Estadística como ciencia. Sugerencias: Busque información sobre el tema en la red y resuma en dos páginas.
Actividad 2.
a- Formule un problema estadístico que revele la manifestación del objeto de estudio de la estadística descriptiva y su importancia para el Licenciado en Educación en la especialidad de Matemática-Física.
b- Determine las variables y las escalas respectivas para cada problema que se está resolviendo.
c- Diseñe el esquema de búsqueda y registro de la información, para ello: determine la población y la muestra y el tipo de dato a obtener y cómo lo va a hacer.
d- Confeccione las matrices y ficheros o archivos de datos.
e- Haga resumen de los datos.
f- Represente gráficamente los datos, según el tipo de variable.
Actividad 3: Realice el cálculo y la interpretación de las medidas estadísticas en el problema planteado.
Actividad 4: Identifiquen cuáles son las variables que pueden ser relacionadas en su problema. Justifique la relación entre ellas. Establezca las relaciones y haga interpretaciones posibles para esos casos particulares.
Sugerencias: Para establecer las relaciones entre variables, usted puede hacer todas, o parte de las acciones que se relacionan a continuación: Confeccione una tabla de doble entrada donde se aprecie la frecuencia absoluta, relativa y marginal y haga la interpretación de los datos; representación en gráficos de: barras dobles o cajas y bigotes de varias variables.; confeccionar un diagrama de dispersión e interprételo; determinar la ecuación de la línea de regresión para el caso estudiado y diga qué resultados le aporta a su investigación o determinar la correlación entre las variables a través de uno de los coeficientes de correlación y explique el resultado obtenido.
Actividad 5: Prepare una exposición de los resultados obtenidos y expóngala al profesor del grupo, significando los aspectos más relevantes y lo aprendido en el desarrollo del proyecto para su trabajo como profesor.
ANEXO 2. Guía para el desarrollo del proyecto en la asignatura Probabilidades y Estadística II (quinto año de la carrera).
En el desarrollo de las actividades de la segunda parte del proyecto, se realizará como continuación del proceso de solución del problema elaborado por usted en cuarto año.
Actividad 1.
a)- En el problema que usted ha venido resolviendo, introduzca la variable: «Estado general del problema» con una escala ordinal cualitativa que incluya los niveles Bien, Regular y Mal.
b)- Usando la combinatoria, determine las formas en que pueden obtenerse cada uno de estos niveles de la escala, a partir de los niveles de las escalas de las variables anteriores.
c)- Dé una evaluación a cada sujeto de la muestra, a partir de los datos con que cuenta.
d)- Construya una tabla de contingencia donde relacione esta nueva variable con una de las anteriores y analice los resultados usando las probabilidades. Para el análisis, se le sugiere que calcule la probabilidad en cada una de las celdas de la tabla y verifique cuál de las situaciones es más probable que ocurra:
I)- Que el sujeto esté en el primer nivel de las dos variables;
II)- Que esté en el nivel más bajo de una y no esté en el nivel bajo de la otra;
III)- Que estén en el nivel más alto de una, dado que estaban en el nivel más bajo de la otra.
Actividad 2.
a)- Determine cuáles son los parámetros poblacionales y los estadígrafos que han de ser estudiados según el problema con que ha venido trabajando.
b)- Plantee un procedimiento de selección muestral adecuado para cada variable.
d)- Determine el tamaño de la muestra para cada variable para una población de tamaño N.
e)- Estime los parámetros poblacionales según convenga. Usted dice para cada una de las variables. Justifique los resultados desde el punto de vista probabilístico.
e)- Seleccione una prueba de hipótesis más conveniente según sea la situación y aplíquela con todos los pasos.
Actividad 3: Prepare una exposición de los resultados obtenidos y expóngala al profesor del grupo, significando los aspectos más relevantes y lo aprendido en el desarrollo del proyecto para su trabajo como profesor.
REFERENCIAS BIBLIOGRÁFICAS
[1] Batanero, C. (2003). Veinte años de conferencias internacionales de educación
estadística. Granada, España: Departamento de Didáctica de las Matemáticas Universidad de
Granada. Recuperado en: https://www.researchgate.net/profile/Carmen_Batanero/publication/282281442_Veinte_anos_de_conferencias_internacionales_de_educacion_
estad'istica_27_CONGRESO_NACIONAL_DE_ESTADISTICA_E_INVESTIGACION_OPERATIVA/links/560cd90308ae6c9b0c42d988.pdf
[2] Díaz Fernández, I., Zurbano Fernández E. y Corral Zapico, C. (2003). Un indicador privilegiado: el porcentaje. España: 27 Congreso Nacional de Estadística e Investigación Operativa, Universidad de Oviedo.
[3] Fiallo, J. (2001). La interdisciplinariedad en la escuela: un reto para la calidad de la educación. La Habana: ICCP.
[4] Gutiérrez, R. B., & i Cintas, P. G. (2001). Mil y una dimensiones del aprendizaje de la Estadísitica. Revista «Estadística Española» 43(148), 189-208
[5] Martinez LLantada, M. (1998). Enseñanza problémica y pensamiento creador. Ciudad de La Habana: Impresión ligera, 27.
[6] Mattana, G. & Castellanos, S. J. (2008). Propuesta interdisciplinaria para el aprendizaje de la estadística en la carrera de pedagogía del Instituto Varzeagrandense de Educación (IVE) Ciudad de la Habana: Editorial Universitaria del Ministerio de Educación Superior de la República de Cuba
[7] Ottaviani, M. G. (1998). Developments and perspectives in statistical education. In Proceedings IASS/IAOS Joint Conference, Statistics for Economic and Social Development, Aguascalientes, Mexico, 1-4 September 1998 (CD-ROM).
[8] Weaver, W. (2003). Matemáticas en el Mundo Moderno1. Selecciones de Scientific American.