
Mendive. Journal on Educación, october-december, 2022; 20(4):1338-1352
Translated from the original in Spanish
Original articleMathematical thinking in early childhood: teaching strategies of preschool educators
Pensamiento matemático en la primera infancia: estrategias de enseñanza de las educadoras de párvulos
Pensamento matemático na primeira infância: estratégias de ensino de educadores de pré-escola
Ana Milena Mujica-Stach1![]() https://orcid.org/0000-0002-4033-0026
https://orcid.org/0000-0002-4033-0026
Maximina Márquez Torres2![]() https://orcid.org/0000-0002-0019-8809
https://orcid.org/0000-0002-0019-8809
1 University of Los Lagos. Education department. Osorno-Chile. ![]() ana.mujica@ulagos.cl
ana.mujica@ulagos.cl
2 University of Los Lagos. Department of Exact Sciences. Osorno-Chile
Received: May 13th, 2022.
Accepted: September 23rd, 2022.
ABSTRACT
Although there are various theories regarding the development of mathematical thinking in early childhood, there is a gap in the application of didactic strategies to enhance its development. The research was aimed at analyzing the essential characteristics of the categories Development of Mathematical Thought and Didactic Strategies, identifying and interpreting the didactic strategies used by nursery educators to develop mathematical thinking in girls and boys, aged between 2 and 4 years, in Chilean classrooms. The sample consisted of 7 key informants, who practice their profession in different regions of Chile. A qualitative method with an interpretive approach was used, which allowed describing, categorizing and theorizing about the realization of the aforementioned constructs. The conclusions highlight the importance of designing didactic strategies that favor the development of mathematical thinking in girls and boys, which is based on the experimentation and interaction of collective, playful and interactive activities that are coupled with pedagogical support. The foregoing makes it possible for the teaching and learning of mathematics to move away from traditional methods, and allow its development as a future thought.
Keywords: Everyday life; educational strategies; Mathematical Thinking; early childhood.
RESUMEN
A pesar de que existen diversas teorías referentes al desarrollo del pensamiento matemático en la primera infancia, existe un vacío en cuanto a la aplicación de estrategias didácticas para potenciar su desarrollo. La investigación estuvo dirigida a analizar las características esenciales de las categorías Desarrollo del Pensamiento Matemático y Estrategias Didácticas, identificando e interpretando las estrategias didácticas que emplean las educadoras de párvulos para desarrollar el pensamiento matemático en niñas y niños, con edades entre 2 y 4 años, en las salas de clases chilenas. La muestra estuvo conformada por 7 informantes claves, quienes ejercen su profesión en distintas regiones de Chile. Se utilizó un método cualitativo con un enfoque interpretativo, lo que permitió describir, categorizar y teorizar sobre la concreción de los constructos anteriormente mencionados. Las conclusiones resaltan la importancia de diseñar estrategias didácticas que favorezcan el desarrollo del pensamiento matemático en las niñas y niños, el cual se cimenta en la experimentación e interacción de actividades colectivas, lúdicas e interactivas que van acopladas con un soporte pedagógico. Lo anterior posibilita que la enseñanza y el aprendizaje de la matemática se aleje de los métodos tradicionales, y permita su desarrollo como un pensamiento futuro.
Palabras clave: Cotidianidad; estrategias educativas; pensamiento matemático; primera infancia.
RESUMO
Embora existam várias teorias sobre o desenvolvimento do pensamento matemático na primeira infância, há uma lacuna na aplicação de estratégias didáticas para potencializar seu desenvolvimento. A pesquisa teve como objetivo analisar as características essenciais das categorias Desenvolvimento do Pensamento Matemático e Estratégias Didáticas, identificando e interpretando as estratégias didáticas utilizadas por educadores de infância para desenvolver o pensamento matemático em meninas e meninos, com idades entre 2 e 4 anos, em salas de aula chilenas. A amostra foi composta por 7 informantes-chave, que exercem sua profissão em diferentes regiões do Chile. Foi utilizado um método qualitativo com abordagem interpretativa, que permitiu descrever, categorizar e teorizar sobre a realização dos construtos supracitados. As conclusões destacam a importância de desenhar estratégias didáticas que favoreçam o desenvolvimento do pensamento matemático em meninas e meninos, que se baseia na experimentação e interação de atividades coletivas, lúdicas e interativas, aliadas ao apoio pedagógico. O exposto permite que o ensino e a aprendizagem da matemática se afastem dos métodos tradicionais e permitam seu desenvolvimento como um pensamento futuro.
Palavras-chave: Cotidiano; estratégias educacionais; Pensamento Matemático; primeira infância.
INTRODUCTION
In the educational field that contains learning experiences, the use of mathematics teaching methodologies has been frequently seen, focused on giving the child a definition or a formula, in solving problems attached to imitation patterns, causing some sometimes the limitation in the use of new strategies that promote the development of mathematical processes. The approach to the construction of mathematical thoughts is linked to cognitive development, since the girl and the boy know, learn and think, which allows us to infer that they are in the presence of an interactionist approach to learning. This differs from the behaviorist when it is stated that not only is learning from external experiences, or only from reason, as indicated by the rationalists, but that knowledge arises from an inseparable interaction between real experience and reason.
Consequently, the stages of cognitive development proposed by Piaget (1979) are affected by two situations that determine the child's actions in learning situations: the first has to do with the interaction between the child and the object, where the interpretation of reality is the product of your already structured mental scheme; and the second has to do with actions where objects and situations influence the child's schemes, modifying them.
Based on the foregoing, from Jean Piaget's cognitive theory, the area of social-logical learning emerges, and it is there that reference is made to the component of mathematical processes with emphasis on the recognition and use of number, and also on relationships that are established between objects and mathematical logical knowledge (classification, serialization and number), space-time knowledge, and representation.
That is why, from didactics, the integration of new knowledge with existing knowledge is achieved, being a very complex process that requires multiple and varied learning situations, time and opportunities, so that girls and boys put into play certain actions, compare, establish relationships, transform, analyze, understand the results, the process to follow, test a possible solution, and justify the results. Because it is necessary to propose, to girls and boys, didactic situations contextualized in the social, as a starting point to plan new problems to pose.
In this sense, the discovery, the exploration, the continued practice, the procedures and the intentional mediation of the adult, will allow the girls and boys to appropriate mathematical learning. For this reason, the mathematical processes that the educator must address are included in the curricula: spaces and geometric shapes, the mean and its magnitudes, the numerical series, weight, capacity, time, and length. Therefore, the purpose of the inquiry emerges from the analysis of the essential characteristics of the a priori categories of the Development of Mathematical Thought and Didactic Strategies, whose purpose is focused on identifying and interpreting the didactic strategies used by preschool educators to develop mathematical thinking. in girls and boys between 2 and 4 years of age, within the classrooms.
The research was carried out under a qualitative approach, supported by the postpositivist paradigm, and the approached method was phenomenological. Different regions of Chile served as the context of the study. A sampling based on criteria was carried out for the selection of key informants, and a total of 7 nursery educators were selected, who make professional life in different educational institutions in the country. The technique to collect information regarding the study phenomenon was the in-depth interview, and its results were analyzed to identify units of analysis, and, in turn, to generate themes, sub-themes and patterns that describe the experiences and the narrative connections of the participants in relation to the Development of Mathematical Thinking and Didactic Strategies.
Psychogenetic Approach from the Reflection of Jean Piaget
The depth of the psychogenetic approach goes beyond simple processes, such as perceiving, remembering, evaluating and interacting with other people (cognitive development). All of these processes are functions that the brain and mind can perform on a routine basis. In this sense, for Piaget (1979), two conceptions predominate in the psychogenetic approach: Piaget's natural perspective, and information processing. From the conception of cognition, the cognitive system is a widely active system, since it is capable of actively assimilating information and selecting what it is interested in adapting to build its own knowledge (assimilation). In other words, the mind is always reconstructing and interpreting the information that comes from the environment to locate it in the individual's mind within its frame of reference; in a certain sense, this approach is more "realistic", since, from his point of view, the cognitive system is more adaptive for the organism (accommodation).
The psychogenetic approach, according to Piaget (1979), constitutes the essential pillar for human knowledge, since it is based on the link between the environment and learning. For its part, the specialized literature explains that, under this approach, relationships are established between the mind (the human psyche) and genesis (or genetics for some); In this way, the main objective of the study was focused in a very special way, on the processes of the mind (thought).
Although some theorists differ in certain aspects with Piaget's epistemological proposals, there are generally points of contact. For example, Vygotsky (1979) was always attentive to the postulates of Piaget's genetic approach as the main contribution to his sociocultural approach. In this regard, Raynaudo and Peralta (2017) highlight the following:
… Vygotsky praises and criticizes various aspects of Piaget's work. He refers to Piaget's work as one of the most complete theories of the development of language and thought. It locates the strengths in obtaining new empirical data, the scientific culture of the psychological fact, its detailed analysis, the classification of the materials, the new clinical method (p. 32).
From the foregoing, it can be said that the development of thought is based on the search for mechanisms that affect the processes of the mind, and, as already mentioned, Piaget (1976) bases the foundations of his scientific approach on the mechanisms of assimilation and accommodation. For his part, Vygotsky (1979) focuses his idea on the internalization of culture. However, this notion of internalization is conceived by him based on an idea recovered from Piaget, that is, that despite opposing some points pointed out by the latter, he defends that "the child's personality develops by internalizing the attitudes of others significant towards him" (Álvarez and Balmaceda, 2020, p. 8).
On these bases, the psychogenetic approach builds its postulates, in higher psychological processes, that is, the internal or natural plane of the individual (the origin or genesis) and its relationship with internalization (although Piaget himself did not coin the term) of the social processes that the same individual links through the aforementioned mechanisms.
In response to this, Arias (2017), based on Piaget's approaches, explains that in the cognitive development of the individual, their previous experiences mediate the subject's confrontation with new knowledge, for which the same author highlights that:
The impact of genetic psychology on the educational area has been important, despite the fact that it was not Piaget's initial idea when formulating the theory to contribute in this field, however, his contributions have been highly regarded in the educational field (p. 836).
Finally, it should be noted that, for Piaget, the brain and the mind (thought) act once the individual faces the environment: these actions, as this learning model describes, contribute to the organization of information in the schemas. mental, which then will be represented by the individual in the social environment where he develops.
Development of Mathematical Thinking in Girls and Boys of Early Childhood
The study of logical-mathematical processes in children has been, for more than three decades, one of the most researched topics in the cognitive development of children. Jean Piaget is the forerunner of the development of mathematical logical thinking. This development is considered as a fundamental basis for the construction of mathematical operations in the individual. However, these processes should not be limited only to mathematical notions, since their understanding goes beyond the mere formulation of operations. In this sense, developing logical-mathematical processes in the child will help him to recognize and understand his own self, the self with the world around him, and how to relate to it.
For a nursery school teacher, it is vital to recognize the importance of developing simple and logical processes in children that will allow them to function within different social contexts. The most important of these is educational, since it is there where you will create circles that will lay your social foundations for a successful future. That is why Piaget emphasizes the idea of strengthening these processes through the interaction of the child with the world, where the teacher must locate strategies appropriate to the evolutionary stage proposed in his theory, and that until today has been the most important contribution for the initial level educator.
In that order of ideas, Nieves et al. (2019) state that:
One of the main objectives of teaching Mathematics is to develop in students a logical, flexible and creative thinking. Rational thought is the object of study of Psychology and Logic, it manifests itself as a cognitive psychic process and as a result (p. 3).
The foregoing reiterates the importance of logical-mathematical development, which Herlina (2015), cited by Nieves (2019), characterizes as "the cognitive process that includes representation, abstraction, creativity and mathematical demonstration" (p. 2). For this reason, the main objective to be achieved by the educator of the initial level would be to find adequate forms of didactics in the teaching of content through games (the playful is the best friend of the educator) using with it, simple analogies, illustrations, modeling, examples, explanations, and demonstrations.
In attention to didactics, Lugo et al. (2019) highlight the following:
... in school contexts lies an inalienable commitment to promote scenarios loaded with strategies to develop logical-mathematical thinking, thus requiring teachers trained in the mastery of basic notions that allow them to design the relevant strategies to enhance this learning (p. 3).
These strategies must be accompanied or supported by the Curricular Bases of Early Childhood Education (BCEP, 2018), since all teaching action must be supported by the grounded theory based on the child's learning. Taking this point of reference, it is highlighted that the BCEP state that in the evolution of learning in the child it is vital that he build his own knowledge through his interaction with the social world, where he consolidates linguistic codes, as well as mathematical, scientific and social.
In summary, the didactic implications in the development of logical-mathematical processes in the child are reflected in the planning of the activities, where the teacher must handle extensive knowledge and expertise about the stage of the child's evolutionary development (Piaget 1991). If the teacher shows weaknesses in such a situation, it would represent for pedagogical practice the impossibility of achieving objectives, which is none other than the child developing a logical-mathematical thinking that will support him in other learning areas.
It should be noted that the research focused on identifying and interpreting the didactic strategies used by preschool educators to develop mathematical thinking in girls and boys between 2 and 4 years of age, within the classroom.
MATERIALS AND METHODS
The research was framed in the post-positivist paradigm with a qualitative approach, since from the empirical phenomenology it was intended to understand the common experiences related to the Development of Mathematical Thought and Didactic Strategies of actors of the educational process in the different Chilean educational regions, with emphasis on some communes. The understanding of this phenomenon tries to generate a theoretical approach that relates the descriptions of mathematical thought and the units of analysis that emerged from the understanding in order to convey the essence of such experience.
Recognition is important in qualitative research, its comprehensive and interpretive nature, but so is validity. As long as the voices of the participants are respected during the research process and the proposed objective is achieved, to that extent a qualitative study is valid. The representation of the expressions of the actors involved in the research process must be the product of mental realities around a defined phenomenon that lead to individual and collective constructs. Lincoln and Guba (1985) consider that reality "is a set of mental constructions of human beings" (p. 5).
Planes of phenomenological reduction
From the phenomenological perspective, the procedure for collecting information translates into a series of steps that begin with the definition of the phenomenon under study, the compendium of the experiences of the participants, the analysis of the various narratives of the participants, the identification of meaning units, until arriving at the theoretical approximation around the phenomenon. The strategy for the interpretation of the findings, specifically for the phenomenological method, was found to be constituted by reduction.
Initially, the first phenomenological reduction was carried out, which made the researchers reflect on prejudices, judgments or any subjective reference in the selection of key informants.
Then, it was necessary to carry out the following activities and actions:
(a) construction of the interview script;
(b) approach to the geographical context for interaction with key informants (application of the second phenomenological reduction);
(c) the application planning was carried out in consensus of the interviews;
(d) application of the interviews, where the recording was used as an instrument for collecting information. In it, records of common experiences were obtained from the voices of the actors;
(e) specific topics were integrated according to the key informants;
(f) the phenomenological observation technique was applied, stripping away prejudices to record reality with deep concentration and attention to everything given at the time of the interview, thus denoting the second phenomenological reduction;
(g) it was possible to understand and reflect on the meaning of the epistemic, axiological and ontological foundations that support the Development of Mathematical Thought and Didactic Strategies; Y
(h) it was decided to assume the use of ATLAS.ti 7 as a technological tool for the analysis, such a procedure implied that the necessary categories for the construction of a theoretical approximation emerged.
The last step consisted in the elaboration of the protocol descriptions, through the faithful transcription of each in-depth interview, as it was presented in its natural context. It is highlighted that, in these protocol transcriptions, the analysis material reflects the point of view of each interviewee, based on the experiences lived, since the experiences expressed by the informants are transcribed.
Compliance with the categorization process was addressed through the steps described below:
1. Development of the general reading on the descriptions that emerged in each protocol, with the purpose of having a broad vision of the written intentions of each of the key informants in relation to the proposed budgets.
2. Definition of emerging units. A new reading of the protocol descriptions was also considered.
3. Denomination of the central themes, from the selection, in a logical way in relation to the expressions handled by the key informants. Here a grouping by similarity is produced to arrive at the essential themes for the construction of the synthesized individual phenomenological categories (phenomenological reduction).
4. Grouping of reflected expressions of the central theme with the help of the ATLAS.ti 7 technological tool to proceed to the construction of the essential themes and synthesized individual phenomenological categories.
5. Integration of particular and general synthesized structures, and with central themes specific to each category and subcategory, with the help of ATLAS.ti 7.
6. Integration of all the particular structures to a general structure that definitively leads to the construction of a theoretical approach on the Development of Mathematical Thought and Didactic Strategies.
RESULTS
For the contextualization of the findings, it is important to describe the regions that constituted the ontological scenario of the investigation, and in this way, there were elements for understanding the perceptions of the 7 selected key informants. Next, the aforementioned description is presented.
Tarapacá Region: in this region it was observed that most of the educators have an average of 4 to 6 years working, most of them working for the National Board of Kindergartens (JUNJI), municipal schools and kindergartens with the Vía modality. Transfer of Funds (VTF). His last training occurred between 2 and 4 years ago, dictated by JUNJI.
Arica and Parinacota Region: in the commune of Arica, there is a group of nursery educators, those who have between 7 and 9 years of service working for JUNJI, VTF, and Local Services of Public Education (Local Services), their last training was more than 4 years ago, dictated by the Pontificia Universidad Católica de Chile (PUC), and they apply strategies based on games and the Reggio Emilia approach. In this region there is another group of educators, with more than 18 years of service, working in private subsidized schools and in local services; his last training took place between 2 and 4 years before, received from the Ministry of Education (Mineduc).
In the Valparaíso Region, which includes the communes of La Serena, San Antonio, Villa Alemana and Cartagena, the average number of years of service ranges between 10 and 12 years, most of them working for subsidized private schools, JUNJI, and municipal schools, having received the last training a year ago, from the Pontifical Catholic University, and JUNJI.
In the 0'Higging Region, made up of the communes of Villa del Mar, Placilla and Rancagua, nursery educators, with service time between 10 and 15 years, work in subsidized private schools, municipal schools, Fundación INTEGRA (INTEGRA), and VTF, being his last training more than 4 years ago.
In the Maule Region, educators from the Villa Alegre and Chanco communes have between 16 and 18 years of service in private subsidized schools and INTEGRA, with more than four years since the last training provided by INTEGRA.
In the Bío Bí o Region, educators work in the communes of Santa Bárbara and Talcahuano. They have an average of 15 years working for INTEGRA, and VTF, receiving their last training 4 years ago from INTEGRA.
In the Ñuble Region: the educator interviewed has worked for more than 18 years in a subsidized private school, and her last training was between 2 and 4 years ago.
The Metropolitan Region includes the communes of Recoleta, Peñalolén, Lampa, Maipú, San Bernardo, Lo Prado, Ñuñoa, Huechuraba, Puente Alto, and La Florida, among others. Here, it was observed that, in the communes of Recoleta, Peñalolén and Huechuraba, educators have been working on average for 18 years, in establishments with municipal dependence, having received the last training between 2 and 4 years before, imparted by the Administration Department of Municipal Education (DAEM). In the communes of Lampa, Maipú, and San Bernardo, the educators have an average of 7 and 9 years working, being of municipal dependency, and VTF; with more than 4 years without receiving training.
In the communes of Lo Prado and Ñuñoa, the average length of service is between 13 and 15 years, being dependent on VTF, Subsidized Individuals, and JUNJI, having up to 4 years without receiving training.
In the communes of Puente Alto and La Florida, educators have between 4 and 6 years of experience, they belong to the Private Subsidized sector, and VTF. His last training was between 2 and 4 years before, received through JUNJI, and the Center for Improvement, Experimentation and Pedagogical Research (CPEIP).
In the communes of Puente Alto and La Florida, the educators have between 2 and 4 years of experience, being from a Subsidized Private dependency, and VTF; approximately the educators have 4 years without receiving training.
In the Region of La Araucanía, with the communes of Temuco and Victoria, educators have been working for between 7 and 9 years, in places dependent on INTEGRA and in subsidized private schools. They have a year since their last training, provided by the Diego Portales University, INTEGRA, and the Seminarium Foundation.
In the communes of Ancud, Osorno, Llanquihue and Puerto Montt, located in the Los Lagos Region, it is found that in Ancud and Osorno the average time of service of educators exceeds 18 years, in establishments with municipal dependency, JUNJI, and private subsidized school, with training received between 2 and 4 years before, which were dictated by the Agency for French Education Abroad (AEFE), and the PUC. In the commune of Llanquihue, educators have an average of 18 years of work, dependent on subsidized private schools, with training given 4 years ago by Mineduc. In the commune of Puerto Montt, there are educators with work experience of 2 to 3 years, and up to 18 years of service, belonging to INTEGRA and municipal schools, with their most recent training occurring 4 years ago, in charge of CPEIP.
In the Aysén Region, in the communes of Cisnes and Aysén, the educators have work experiences ranging from 12 to 18 years old, from municipal dependency and VTF, having more than 1 year without training.
Lastly, in the Region of Magallanes, in the commune of Punta Arenas, the educator has experience between the ages of 12 and 18, works in a subsidized private school, and her last training took place a year ago.
In the study, it was preliminarily observed that, due to the type of institution that provides the educational service, JUNJI, VTF and INTEGRA present the greatest burden of responsibility, being followed by the municipal schools, and both private subsidized schools and private schools having a lower share. local services. Regarding the length of service, the highest range is located in those with more than 18 years of experience. Along these same lines, in order to gain an in-depth understanding of the essence of the emerging phenomenon between the didactics of mathematics and the development of mathematical thinking in early childhood children, the information collected is presented in a representative structure that largely describes the emerging relationships between the Didactic Strategy category and the subcategories Concrete Actions, Daily Activities, and Base Games. Next, Figure 1 is presented, with the emerging structure:
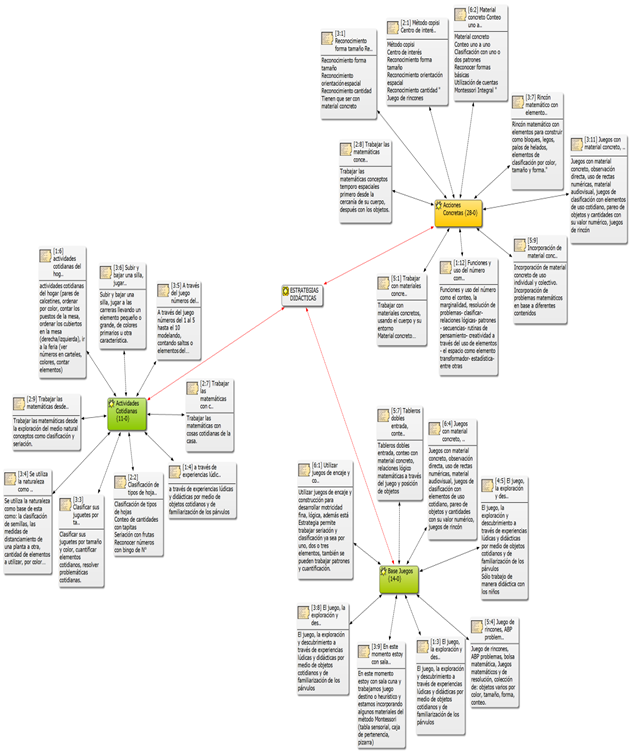
Fig. 1- Particular Structure of the Emerging Didactic Strategy Category
Addressing the complexity of the didactic strategies that promote the development of mathematical thinking in girls and boys in Initial Education is essential, since at the teaching level it is also necessary to contextualize, update or develop the didactic competence to approach the pedagogical encounters together with the promotion of mathematical thinking. The didactics of mathematics should reveal them as a science useful to the human being, and, above all, for the generation of ways of thinking and reasoning that require greater complexity and a greater propensity towards abstraction, as a way of solving problems of the human environment.
With the development of the research, a theoretical approach was generated that related the descriptions and the units of meaning, in order to transmit the essence of the experience in terms of mathematical thinking and the need for didactics that has a great impact on educational communities. of the regions studied.
Based on the previous concerns and statements, a cognitive effort was made to achieve the purpose of this inquiry, which emerges from the interpretation and analysis of the essential characteristics of the a priori categories Development of Mathematical Thought and Didactic Strategies, whose purpose is focuses on identifying and interpreting the didactic strategies used by nursery educators in order to develop mathematical thinking in children between 2 and 4 years of age in the classroom.
In this sense, the Didactic Strategies category is made up of the essential characteristics or subcategories of concrete actions (as shown in Figure 1), daily activities, and base games; From the concretion of these three elements, it can be defined that the didactic strategies that promote the development of mathematical thinking in Early Childhood Education students suppose, according to Feo (2018), "an ideal mental projection focused on an academic or instructional purpose" ( p. 198), which supported by theoretical assertions that define the teaching and learning processes, seek support in procedures and the activation of elementary cognitive processes to process information and generate essential concepts that allow the girl and the boy to recognize shapes, quantity and spatial orientation, which is grouped in a mathematical thought.
As Concrete Actions, all the interactions and stimuli that the child reaches when manipulating, exploring and experimenting with objects, instruments or didactic materials typical of the child's environment can be defined. It should be noted that the educator carries out an immediate pedagogical practice in real situations that the girl or boy faces on a daily basis (BCEP, 2018). This concept is described through the following verbalizations of the key informants interviewed:
P 1: Counting one by one, sorting with one or two patterns, recognizing basic shapes, using accounts (11:14) Functions and use of number, such as counting, marginality, problem solving- sorting- logical relationships- patterns - sequences- thought routines- creativity through the use of elements- space as a transforming element- statistics- among others (20:20).
P 2: COPISI method, center of interest, size shape recognition, spatial orientation recognition, quantity recognition, game of corners (7:12). Classify, patterns, manipulate objects, series, scientific method, cause and effect, heuristic game (18:18). Work on mathematics, space-time concepts, first from the proximity of your body, then with objects (24:24).
P 3: Recognition of size shape, recognition of spatial orientation, recognition of quantity, they have to be with concrete material (5:8). Math corner with buildable items like blocks, legos, popsicle sticks, sort items by color, size and shape (16:16).
P 4: Through concrete material, with his own body (7:8). COPISI method, this strategy is the one we use the most at the institutional level of schools (20:20).
P 5: Work with concrete materials, using the body and its concrete material environment to classify, group (5:6). Functions and use of number such as counting, marginality, problem solving -classifying- logical relationships-patterns- sequences-thinking routines- creativity through the use of elements- space as a transforming element- statistics- among others (22: 22).
P 6: Concrete material, count one by one. Classification with one or two patterns, recognize basic shapes, use of beads, Montessori Integral (6:11). Develop it with concrete material, relevant COPISI method, through challenges (ABP) (8:8).
Mathematical thinking refers to the use of human reason, for which the subject generates the ability to analyze and process information captured by the senses, and in this way, to the extent of their cognitive development, it is possible to establish conclusions, which they are seen as decision-making and actions in search of solving a problematic situation or the demand of a task. In early childhood (Bautista et al., 2018; Mineduc, 2018) the cognitive basis for the development and strengthening of thought is formed, and there is an invariable connection with the evolutionary characteristics, interests and needs of girls and boys.
P 1: Daily activities at home (pairs of socks, ordering by color, counting places on the table, ordering cutlery on the table (right/left), going to the fair (see numbers on posters, colors, count items) (9:9).
P 2: Children protagonists in the construction of their learning (19:19). Work mathematics from the exploration of the natural environment, concepts such as classification and seriation (25:25).
P3: Classify their toys by size and color, quantify everyday items, solve everyday problems (12:12). Nature is used as a basis for: the classification of seeds, the distance measures from one plant to another, the number of elements to be used, by color, size, etc. (13:13). Raise and lower a chair, play races carrying a small or large element, of primary colors or another characteristic (15:15). Through daily activities the girl and the boy interact and learn, from this it is inferred that said actions The didactic plan planned by the teacher is composed or supported by guiding premises for the compilation, organization, analysis of peculiar situations learned socially to generate a decision-making or some conclusion (Feo, 2014).
The Games Base is all game action planned as a didactic means for meaningful learning to emerge. The game (Ponce, 2017; Mineduc, 2018; and González-Moreno, 2018), in other words, is the guiding activity intended for didactic purposes that is used for the development of mathematical thinking based on play, whose purpose is to activate cognitive processes such as abstraction, representation, creativity and mathematical demonstration. In this sense, the key informants express the following:
P 1: The game, exploration and discovery through playful and didactic experiences through everyday objects and familiarization of toddlers (8:8). Various games to develop mathematical thinking (17:17).
P 2: The game as a means of learning (20:20).
P 3: The game, exploration and discovery through playful and didactic experiences through everyday objects and familiarization of infants (17:17).
P 4: Play, exploration and discovery through playful and educational experiences through everyday objects and familiarization of toddlers I only work in a didactic way with children (14:15).
P 5: Double entry boards, counting with concrete material, logical-mathematical relationships through the game and position of objects (20:20).
P 6: Use matching and building games to develop fine motor skills, logic; In addition, this Strategy allows to work serialization and classification, either by one, two or three elements, patterns and quantification (5:5) can also be worked on.
P 7: All based on the game and Reggio-Emilia approach (7:7).
Finally, the promotion of the development of mathematical thinking in girls and boys of Initial Education stimulates and gives priority to reasoning glimpsed by cognitive processes such as understanding, analysis, comparison, estimation, spatial imagination, seen in turn as the essential axis for own development of mathematical skills.
DISCUSSION
According to the findings, it is evident that mathematical logical thinking is conceived as a cognitive process and implies developing skills for the acquisition of knowledge in boys and girls in early childhood, and is not necessarily directed to the basic processes of mathematics, but it is also a process that allows the evolution of other areas of learning. Hence, Piaget (1991), maintains that the boy and the girl, according to their development, learn from a logical sequence, which allows the assimilation of the elements that surround them with their own structures that give way to other states. evolutionary, therefore mathematical logical knowledge arises from the first months of life when the baby is having experiences when manipulating objects, which allows to go to a progressive knowledge of the world, from the simplest to the most complex.
Therefore, the study in the context of Early Childhood Education, achieves that girls and boys develop their mathematical thinking in the best way, in an environment where the teaching action allows, from creativity, to design didactic strategies, and to use diverse strategies to solve real problems, involving the development of skills, attitudes, values, and useful and necessary knowledge from individual or collaborative work, promoting, in turn, reasoning, analysis, appreciation, spatial imagination, association, classification, seriation, and inclusion, in order to generate possibilities for the construction of mathematical concepts that allow the girl and the boy to recognize shapes, quantity, and spatial orientation.
The findings allowed to reveal that, apart from recognizing the need to use didactic strategies in mathematics as the foundation of its didactic specificity, it is possible to achieve a broad and consolidated mathematical thought towards continuous development. It should be noted that there are authors who express that the greatest difficulty in teaching mathematics in early childhood has to do with the strategies applied by teachers (Celi et al., 2021).
The above reflects the importance of considering that daily activities in classroom environments are defined by a series of procedures and operations with which the girl or boy is familiar and are typical of their social and cultural environment. The child is born in a social context that shelters and educates him, through customs and traditions, as well as the demands of that same environment. Hence, the daily activities that are part of the didactic strategies that promote the development of mathematical thinking in preschool children are fundamental and focus their importance on raising the child's awareness of the usefulness and use of mathematical thinking in human life.
BIBLIOGRAPHIC REFERENCES
Álvarez, A y Balmaceda, C. (2020). El concepto dialéctico de interiorización en Vygotsky: aproximaciones a un debate. Psicología, Conocimiento y Sociedad, 8(1), 4-29. Disponible en: doi:10.26864/pcs.v8.n1.2
Arias, P. (2017). Análisis de la Teoría de Psico-genética de Jean Piaget: Un aporte a la discusión. Revista Científica Dominio de las Ciencias, 3(3), 1-13. Disponible en: doi:10.23857/dc.v3i3.508
Bautista, L., Del Río, M. y Susperreguy, M. (2018). ¿Qué hacen las educadoras de párvulos para enseñar matemáticas? Un estudio en salas chilenas. Bordón Revista de pedagogía. 70(3), 1-17. Disponible en: https://doi.org/10.13042/Bordon.2018.63132
Celi, S., Sánchez, V., Quilca, M. y Paladines, M. (2021). Estrategias didácticas para el desarrollo del pensamiento lógico matemático en niños de educación inicial. Horizontes Revista de Investigación en Ciencias de la Educación, 5(19), 826-842. Disponible en: https://doi.org/10.33996/revistahorizontes.v5i19.240
Feo, R. (2014). Desde el Aprendizaje Estratégico Hacia la Formación Docente. Revista Gaceta de Pedagogía, 33(1), 102 -124. Disponible en: https://gacetadepedagogia.jimdofree.com/revista-n%C2%BA-33-a%C3%B1o-2014/5-ronald-feo-mora/
Feo, R. (2018). Diseño de situaciones de aprendizaje centradas en el aprendizaje estratégico. Tendencias Pedagógicas, 31(1), 187-206. Disponible en: https://doi.org/10.15366/tp2018.31.011
González-Moreno, C. (2018). El juego como estrategia para el desarrollo del lenguaje en un niño con Trastorno del Espectro Autista desde el ámbito de la educación inclusiva. IE Revista de investigación educativa de la REDIECH, 9(17), 9-31. Disponible en: http://orcid.org/0000-0001-8099-8605
Lincoln, Y. y Guba, E. (1985). Naturalistic inquiry. Sage Publication.
Lugo, J., Vílchez, O. y Romero, L. (2019). Didáctica y desarrollo del pensamiento lógico matemático. Un abordaje hermenéutico desde el escenario de la educación inicial. Revista Logos Ciencia & Tecnología, 11(3), 18-29. 2019. https://doi.org/10.22335/rlct.vlli3.991.
MINEDUC. (2018). Bases Curriculares Educación Parvularia. Mineduc: Chile
Nieves, S., Caraballo. C. y Fernández, C. (2019). Metodología para el desarrollo del pensamiento lógico-matemático desde la demostración por inducción completa. Mendive. Revista de Educación, 17(3), 393-408. Disponible en: https://mendive.upr.edu.cu/index.php/MendiveUPR/article/view/1681
Piaget, J. (1976). El compartimento, motor de la evolución. Gallimard.
Piaget, J. (1979). El mecanismo del desarrollo mental. Editora Nacional
Piaget, J. (1991). Seis estudios de psicología. Labor.
Ponce, M. (2017). Juego, libertad y movimiento. Ediciones de la Junji. Chile
Raynaudo, G. y Peralta, O. (2017). Cambio conceptual: una mirada desde las teorías de Piaget y Vygotsky. Revista Liberabit, 23(1), 110-122. Disponible en: https://doi.org/10.24265/liberabit.2017.v23n1.10
Vygotsky, L. (1979). El desarrollo de los procesos psicológicos superiores. Grijalbo.
Conflict of interests:
The authors declare not to have any interest conflicts.
Authors contribution:
The authors have participated in the design and writing of the work, and analysis of the documents.
![]() This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License
Copyright (c) Ana Milena Mujica-Stach, Maximina Márquez Torres