El pensamiento lógico-matemático del estudiantado. ¿Un asunto didáctico?

El pensamiento lógico-matemático del estudiantado. ¿Un asunto didáctico?

Los rendimientos obtenidos en Ecuador en el informe del Programa Internacional de Evaluación de Estudiantes administrado por la Organización para la Cooperación y Desarrollo Económicos en 2018, la prueba Ser Bachiller; y, recientemente, el Examen de Acceso a la Educación Superior, revelan una profunda debilidad en el aprendizaje y desarrollo de capacidades para la resolución de problemas. El acervo metodológico del profesorado no está ayudando a solucionar esta cuestión, razón por la que el presente artículo tiene como objetivo analizar las estrategias didácticas creativas y el pensamiento lógico-matemático de los adolescentes de una institución educativa fiscal en el cantón Portoviejo. Se realizó un estudio cuantitativo de nivel descriptivo y correlacional para determinar hallazgos que faciliten la explicación de esta situación problémica. En el trabajo de campo se aplicó una batería de preguntas para los estudiantes y una encuesta para los docentes del área de matemáticas. Los resultados demuestran que el 85.7 % de los adolescentes tienen una calificación inferior a 7, lo que significa que no han superado los niveles de aprendizaje requeridos en la resolución de problemas. Por su parte, los docentes utilizan procesos didácticos creativos con mucha frecuencia, pero con un tiempo limitado para que los estudiantes reflexionen sobre las posibles soluciones de un problema. El docente asume una gran responsabilidad en el proceso de aprendizaje de las matemáticas, porque es el mediador de construir esos conocimientos para que los estudiantes puedan comprenderlos.

Palabras clave: estrategias didácticas creativas; material didáctico; pensamiento creativo; pensamiento lógico-matemático; proceso didáctico.

The obtained results in Ecuador in the report of the International Student Assessment Program administered by the Organization for Economic Cooperation and Development in 2018, the Ser Bachiller test; and, recently, the Higher Education admission exam reveals a deep weakness in learning and developing problem-solving skills. The methodological heritage of teachers is not helping to solve this issue, which is why this article aims to analyze the creative didactic strategies and the logical-mathematical thinking of adolescents from a public school in Portoviejo canton. A descriptive and correlational quantitative study was carried out to determine findings that facilitate the explanation of this problematic situation. In the fieldwork, a bank of questions was applied to students and a survey was applied to math teachers. The results show that 85.7 % of adolescents have a score lower than 7, which means that they have not exceeded the required learning levels in problem-solving. For their part, teachers use creative didactic processes very frequently but with limited time for students to reflect on possible solutions to a problem. The teacher assumes a great responsibility in the mathematics learning process because he is the mediator of building that knowledge so that students can understand it.

Keywords: creative teaching strategies; teaching materials; creative thinking; mathematical logical thinking; didactic process.

Os resultados obtidos no Equador no relatório do Programa Internacional de Avaliação de Estudantes administrado pela Organização para Cooperação e Desenvolvimento Econômico em 2018, o teste Ser Bachiller; e, recentemente, o Exame de Admissão ao Ensino Superior revela uma profunda fraqueza na aprendizagem e no desenvolvimento de habilidades de resolução de problemas. A herança metodológica dos professores não está ajudando a resolver esta questão, razão pela qual este artigo tem como objetivo analisar as estratégias didáticas criativas e o pensamento lógico-matemático de adolescentes de uma instituição de ensino fiscal no cantão de Portoviejo. Foi realizado um estudo quantitativo descritivo e correlacional para determinar achados que facilitem a explicação dessa situação problemática. No trabalho de campo, foi aplicada uma bateria de perguntas aos alunos e um questionário aos professores da área de matemática. Os resultados mostram que 85,7% dos adolescentes têm nota inferior a 7, o que significa que não ultrapassaram os níveis de aprendizagem exigidos na resolução de problemas. Por sua vez, os professores utilizam com muita frequência processos didáticos criativos, mas com tempo limitado para que os alunos reflitam sobre possíveis soluções para um problema. O professor assume uma grande responsabilidade no processo de aprendizagem da matemática, pois ele é o mediador da construção desse conhecimento para que os alunos possam compreendê-lo.

Palavras-chave: estratégias criativas de ensino; material didático; pensamento criativo; pensamento lógico-matemático; processo didático.

El pensamiento lógico es esencial en el ámbito educativo por la connotación que tiene en las diferentes áreas de conocimiento, pues hace posible que los estudiantes contemplen diversos puntos de vista, expresen criterios concretos y establezcan resoluciones oportunas.

Fortalecer el pensamiento es primordial en el proceso de enseñanza en los estudiantes, ya que contribuye a adquirir conocimientos y les ayuda a apropiarse de la resolución de operaciones lógicas. Por esta razón, es importante que los niños integren este aprendizaje desde la etapa de preescolar, para que alcancen un óptimo desenvolvimiento en el manejo de las matemáticas.

La prueba PISA-D (2018) se realizó en el Ecuador "con la finalidad de evidenciar la realidad académica, especialmente en la resolución de problemas matemáticos, pues el 70.9 % de los estudiantes del país no alcanzan el nivel 2 (nivel de desempeño básico¹)" (p. 44).

De acuerdo con el Ministerio de Educación (2016), el currículo de matemáticas contempla que "la enseñanza de la Matemática tiene como propósito fundamental desarrollar la capacidad para pensar, razonar, comunicar, aplicar y valorar las relaciones entre las ideas y los fenómenos reales (…)" (p. 52).

Por ser un tema de interés académico se procedió a realizar una revisión documental, a fin de exponer investigaciones de similares características al tema de estudio, las cuales servirán como antecedente de la investigación.

La didáctica creativa es un conjunto de estrategias que permite facilitar el aprendizaje de los estudiantes.

En la educación es importante y fundamental incentivar el pensamiento creativo en los estudiantes, además, debe ser considerado como una herramienta imprescindible en el proceso de enseñanza aprendizaje.

El éxito del proceso didáctico depende del conocimiento, capacidad y desempeño del docente para realizarlo con diferentes actividades adecuadas, que tienden a la consecución del mismo fin, que es facilitar los aprendizajes de los estudiantes.

Es necesario que el docente utilice material didáctico que contribuya al desarrollo de los procesos didácticos. Por otra parte, el uso de la tecnologia ayudará al estudiante a desarrollar su destreza y a mejora el rendimiento académico.

En el ámbito de la enseñanza-aprendizaje en el aula, existe un sinnúmero de factores que intervienen en los procesos didácticos a fin de garantizar los mejores resultados de los estudiantes. Dentro de la gama de agentes participantes en los ambientes educativos se encuentran los recursos didácticos, considerados como parte fundamental del diseño curricular (…), por otro lado, las nuevas tecnologías han cambiado nuestra forma de acceder a la información, la manera de interactuar con ella, así como la manera de aprender con y de ella. Procurar que los ambientes de aprendizaje junto con el profesor consideren estos cambios y se adapten a la realidad actual de la comunicación del estudiante digital podría resultar benéfico (Trejo González, 2018, pág. 619).

Para Celi, Quilca, Sánchez y Paladines (2021), el pensamiento lógico-matemático es:

Este artículo se propone analizar las estrategias didácticas creativas que aplican los docentes y el pensamiento lógico-matemático de los adolescentes. Además, se pretende alentar a los profesores para que estimulen en el alumnado la capacidad de proponer y solucionar inconvenientes con una diversidad de métodos, estrategias y técnicas activas; así como, de recursos estimulantes, no solo como instrumento de aplicación, sino también como una base del enfoque general para el trabajo de cada uno de los períodos del proceso de educación y aprendizaje en el área de matemáticas.

Este trabajo de investigación se elaboró a partir de un diseño no experimental, con técnicas cuantitativas de corte transversal y de nivel descriptivo y correlacional. El estudio no comprometió el manejo de las variables, sino que recogió información directamente de las fuentes primarias para determinar los resultados que se expresan en el análisis de este artículo. Fue de carácter transversal, por cuanto se tomó como referencia un corte en el tiempo y una recogida de datos que se comparó consigo misma. El estudio posee una parte descriptiva con medidas de tendencia central, para explicar las variables de la primera categoría -estrategias didácticas creativas-. La segunda categoría (pensamiento lógico-matemático) se analizó mediante cálculos de tendencia central y correlaciones de las variables evaluadas como dimensiones de la categoría de estudio.

La investigación se llevó a cabo en una institución fiscal de la ciudad de Portoviejo, con una población estudiantil que se compone de 325 estudiantes mujeres y 204 varones legalmente matriculados. La institución cuenta con 10 profesores de Matemática en el subnivel de Educación Básica Superior. El tamaño de la muestra requirió de 222 estudiantes participantes, considerando un margen de error del 5 % y el 95 % de confianza. Los sujetos fueron seleccionados mediante un muestreo aleatorio simple y para el profesorado se contempló el universo de la institución.

El instrumento que se utilizó para la recolección del material de la primera categoría fue una encuesta de base estructurada con 11 preguntas orientadas a la exploración del uso de la tecnología desde los principios de la creatividad. Esta encuesta se constituyó de 11 variables que se recalcularon en función de las respuestas para interpretar los datos obtenidos.

Para la recogida de información de la segunda categoría se utilizó la batería de pensamiento lógico en etapa formal, un instrumento que consta de seis dimensiones: seriación, clasificación, identificación, lateralidad, correspondencia y comparación. Cada dimensión se estructura en cinco ejercicios graduados con los que se puede valorar el grado de madurez de las habilidades intelectuales requeridas para la resolución de problemas en el estadio del pensamiento formal. El cuestionario se sometió al coeficiente alfa de Cronbach y recabó una puntuación global de 0.79, lo que determina un adecuado grado de confianza en su estructura. Esta prueba se aplica a sujetos que tienen entre 12 y 15 años o que están cursando el nivel o grado correspondiente al subnivel de Educación Básica Superior del Sistema Nacional de Educación ecuatoriano.

El instrumento se valora por dimensiones en una escala del 1 al 10, cuyo valor de aprobación aceptado en este estudio es siete, que se ha cuantificado en función del porcentaje acumulado que se calculó de la muestra para validación. Es recomendable realizar comparaciones de las medias obtenidas por los sujetos evaluados para establecer diferencias significativas entre los grupos.

Para el análisis de datos se cuantificaron las medidas de tendencia central de los datos. En la primera categoría (uso creativo de la tecnología) se calculó la frecuencia relativa de las respuestas obtenidas de la aplicación de la encuesta. Para representar las dimensiones se procedió a recalcular una variable integradora, tal y como se representa en los gráficos 1 a 4 como resultantes de las variables incluidas en esta.

En cuanto a la segunda categoría, las variables evaluadas se integran en las dimensiones que evalúa el instrumento. En primera instancia, se calcularon las medidas de tendencia central del resultado global de la escala (media, moda, desviación, mínimo, máximo y percentiles). Luego se valoraron las tendencias centrales de los desempeños por cada dimensión, para realizar un análisis detallado de las capacidades lógicas exploradas en este estudio.

Finalmente, se calculó la correlación de Pearson en los resultados de las dimensiones evaluables de la escala de pensamiento lógico. Con estos datos se determinaron las conclusiones del estudio y las relaciones existentes entre la metodología aplicada para la investigación, el uso de diagramas de flujo y las capacidades del pensamiento lógico que se involucran en el aprendizaje matemático de los adolescentes.

La encuesta tuvo la finalidad de explorar los procesos didácticos creativos que aplica el profesorado en el proceso de enseñanza-aprendizaje en las matemáticas, para lo cual se tomó una población de 10 docentes que imparten esta asignatura en la institución educativa.

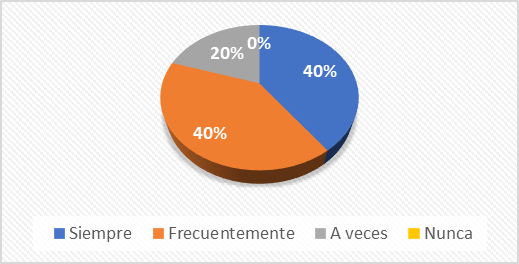
Gráf. 1- Reflexión de las posibles soluciones
Fuente: elaboración propia. Encuesta dirigida a los docentes del área de matemáticas de una institución educativa fiscal de la ciudad de Portoviejo

En la encuesta se indagó acerca del tiempo y espacio que los docentes brindan a sus estudiantes para que reflexionen sobre sus respectivas soluciones a un problema. El gráfico 1 refleja que un 40 % lo hace siempre y frecuentemente, mientras que un 20 % solo a veces. Es importante mencionar que, dentro del salón de clase, los profesores tienen el reto de animar a los alumnos para que expresen su opinión sobre lo que piensan respecto a lo que han aprendido, ya que de esta forma descubrirán cómo reflexionar por cuenta propia.

Gráf. 2- Uso de preguntas para la exploración de los problemas
Fuente: elaboración propia. Encuesta dirigida a los docentes del área de matemáticas de una institución educativa fiscal de la ciudad de Portoviejo

Por otro lado, los resultados estadísticos del gráfico 2 exponen que el 30 % de los docentes plantean interrogantes sobre el significado de las representaciones realizadas por los estudiantes en la resolución de un problema; un 50 % lo hace frecuentemente, y un 20 % a veces. Así, se infiere que los docentes no están aplicando la indagación en los saberes, y este es un espacio apropiado para hacer un monitoreo sobre el nivel de conocimiento del estudiante sobre los contenidos explicados.

Gráf. 3- Metarreflexión del proceso de resolución de problemas
Fuente: elaboración propia. Encuesta dirigida a los docentes del área de matemáticas de una institución educativa fiscal de la ciudad de Portoviejo

Como se puede observar en el gráfico 3, un 30 % de los docentes recuren a la motivación para estimular a sus estudiantes en el desarrollo de procesos matemáticos; un 50 % lo hace frecuentemente, y el 20 % a veces. Estos datos evidencian insuficiencia por parte de los docentes, si bien no permiten a los estudiantes reflexionar acerca de cómo han llegado a un resultado o solución a partir de su propia experiencia.

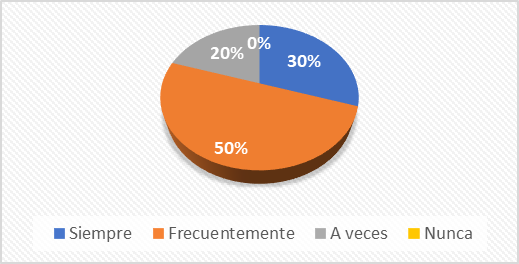
Gráf. 4- Nuevos conceptos y explicaciones
Fuente: elaboración propia. Encuesta dirigida a los docentes del área de matemáticas de una institución educativa fiscal de la ciudad de Portoviejo

De los datos del gráfico 4 se desprende que el 30 % de los docentes autorizan al alumnado a poner en práctica nuevos conceptos para que elaboren explicaciones que constituyan la solución al problema, mientras que un 50% lo hace frecuentemente, y el 20% a veces. Al presentar un porcentaje bajo en este criterio los estudiantes tendrán dificultades para formular o plantear nuevas situaciones de problemática y de interrogantes. Consolidación de los procesos de pensamiento lógico en la resolución de problemas

N	Válidos	222
	Perdidos	0
Media		4.82
Moda		4.00
Desv. Desviación		2.07
Asimetría		0.45
Error estándar de asimetría		0.27
Mínimo		0.00
Máximo		9.67
Percentiles	25	3.33
	50	4.67
	75	6.00

Nota: la equivalencia es el promedio de los puntajes obtenidos en cada dimensión de la batería de pensamiento lógico

El 85.7 % de los estudiantes ha obtenido una calificación inferior a 7.00 en la equivalencia de puntaje de la batería de pensamiento lógico-matemático. El puntaje medio del rendimiento de los estudiantes equivale 4.82 sobre 10, con una desviación estándar de 2.07, lo que implica que existe amplia distancia entre las anotaciones alcanzadas por los estudiantes en el instrumento. La moda de los resultados equivale a 4.00; esto significa que están en un percentil de rendimiento menor al 50 %. La nota mínima de los estudiantes equivale a 0.00 y la mayor calificación es de 9.67. A tenor de lo mencionado, se podría describir que existen estudiantes con alta consolidación en su pensamiento lógico para la resolución de problemas, como también otros con muy bajo rendimiento.

Tabla 2- Resultados por dimensiones de la batería de pensamiento lógico en etapa formal

		Seriación	Identificación	Clasificación	Lateralidad	Correspondencia	Comparación
N	Válidos	222	222	222	222	222	222
N	Perdidos	0	0	0	0	0	0
Media		3.74	7.82	4.49	4.68	3.82	4.49
Moda		4.00	10.00	4.00	4.00	4.00	4.00
Desv. Desviación		2.30	2.78	2.92	2.61	2.68	3.18
Asimetría		1.06	-1.20	0.36	0.55	0.41	0.27
Error estándar de asimetría		0.27	0.27	0.27	0.27	0.27	0.27

Una vez aplicada la batería, con los datos obtenidos por categorías, se aprecia que la dimensión mejor puntuada fue la de identificación, con una media de 7.82 y una desviación estándar de 2.78; en este caso no hay normalidad en la distribución de los datos. Los valores se vuelven inestables y el rango entre las agrupaciones de estudiantes es muy amplio. Por su parte, la dimensión seriación fue la más baja de todas, con una media que equivale a 3.74 y desviación estándar de 2.30; aquí, la distribución de datos no se ajusta a la normalidad. Asimismo, estos resultados nos permiten describir que, desde la dimensión de la seriación, el 100 % del grupo evaluado tuvo un puntaje igual o menor a 10 puntos sobre 10. Se nota que la distribución se ajusta a la normalidad y los valores se ratifican con el promedio mencionado en la tabla 2. En la dimensión de identificación se observa que los datos no se ajustan a la normalidad, si bien el 50.6 % del estudiantado recibió puntuaciones iguales o menores a 8. Para la dimensión de clasificación, el 90.9 % de la población consignó esta anotación. En la prueba de lateralidad se evidenciaron resultados del 90.9 % con calificaciones iguales o menores a 8; en correspondencia el 96.1 %, y en comparación el 87 %.

Tabla 3- Correlación de las dimensiones de la batería de pensamiento lógico en etapa formal

	Seriación	Identificación	Clasificación	Lateralidad	Correspondencia	Comparación
Seriación	1	.454**	.645**	.521**	.496**	.506**
Identificación	.454**	1	.550**	.257*	.385**	.499**
Clasificación	.645**	.550**	1	.494**	.502**	.534**
Lateralidad	.521**	.257*	.494**	1	.538**	.587**
Correspondencia	.496**	.385**	.502**	.538**	1	.647**
Comparación	.506**	.499**	.534**	.587**	.647**	1
**. La correlación es significativa en el nivel 0.01 (unilateral)
*. La correlación es significativa en el nivel 0.05 (unilateral)

Las repercusiones de la aplicación de la batería de pensamiento lógico vertieron resultados en etapa formal de acuerdo con la prueba de correlación de Pearson, que demuestra que las variables se correlacionan fuertemente entre sí. Esto podría interpretarse como una fortaleza colectiva en el pensamiento lógico de los adolescentes evaluados.

De la etapa diagnóstica aplicada a los docentes se logró determinar que ellos no siempre aplican los procesos didácticos creativos en la enseñanza y aprendizaje. Con base en esta investigación, surge el siguiente análisis: respecto al criterio de reflexión de las posibles soluciones, se manifiesta un porcentaje medio de aplicación, algo preocupante, ya que la faceta reflexiva implica que el profesor facilite y promueva una reflexión constante de los estudiantes sobre cómo asimilan, cómo pueden aprender mejor y con qué recursos, además de brindar herramientas y oportunidades para planificar, monitorear y evaluar su propio proceso.

Con lo expuesto anteriormente, podemos citar a Prieto, M. N. (2021): (…) "La reflexión supone una capacidad, una consciencia de nuestras acciones, un proceso que es enriquecedor si permite las transformaciones en nuestras prácticas cotidianas para la mejora de los procesos de enseñanza y aprendizaje" (p. 101).

or otro lado, Delgado (2019) manifiesta que: "Las reflexiones de los alumnos pueden ayudar a los maestros a modificar y planificar lecciones futuras, ver qué estrategias están ayudando y qué alumnos necesitan atención adicional y qué conexiones establecen entre la lección y lo que ven fuera del aula" (párr. 14).

Con relación al criterio sobre el recurso de las preguntas para explorar los problemas, se puso de relieve que siempre las formulan un porcentaje mínimo de profesores. En la enseñanza de las matemáticas, las preguntas son un instrumento de suma importancia para el desarrollo del pensamiento lógico, por lo que se aplaude la gran labor del docente para generar espacios de discusión o formulación de preguntas de manera personal en torno al tema tratado. Se podría sugerir que, para la aplicación de las destrezas o estrategias, el profesorado debe de tener en cuenta la formulación de preguntas, ya que es un modo de generar un diálogo con los estudiantes y, a la vez, propiciar un ambiente de confianza para que ellos puedan contestar sin ningún temor.

En cuanto al criterio de metarreflexión del proceso de resolución de problemas, se puede decir que los docentes de matemáticas lo adoptan en un porcentaje mínimo, aunque un número razonable de ellos lo hace con frecuencia. La reflexión está siempre presente durante la interacción del estudiante y el profesor, pues establece una relación mediática con el conocimiento. Es crucial crear un ambiente de tranquilidad para facilitar la concentración a la hora de plantear el análisis de un problema.

Dentro del proceso de aprendizaje de los estudiantes es vital que el docente sepa explicar los pasos que han de seguirse en la resolución de un problema. Esto se hará mediante un orden jerárquico y sin omitir ciertas pautas de resolución, lo que supone que el alumno se apropie de su propio conocimiento.

En vista del criterio de nuevos conceptos y explicaciones, se apreció que un porcentaje mínimo de los docentes lo aprovechan. Al limitarlos, estamos evitando que los estudiantes puedan indagar, investigar, proponer o simplemente no aplicar estrategias para la solución de un problema.

Desde la perspectiva de Barrera, Reyes, Campos y Rodríguez (2021): "La resolución de problemas es el medio ideal para aprender matemáticas, ya que los estudiantes, en su fase de formación, pueden realizar experimentos con objetos matemáticos, formular y justificar conjeturas, así como plantear nuevas situaciones problemáticas o interrogantes, actividades que integran los ejes experimental e inductivo de la disciplina" (p. 11).

Tras la aplicación de la batería de pensamiento lógico en etapa formal a 222 adolescentes de una institución educativa y tras comprobar sus resultados, se concluye que no existe un grado aceptable en la capacidad para resolver problemas matemáticos. Esta afirmación se corrobora con la evidencia del bajo porcentaje de docentes que no emplean siempre los procesos didácticos creativos, según los rendimientos que arrojó la indagación en el ámbito docente. Cabe resaltar que estos métodos constituyen estrategias para un aprendizaje constructivista que, con ayuda de la tecnología y materiales didácticos, son de gran ayuda para que los estudiantes generen un buen desarrollo cognitivo a través del razonamiento, la creatividad y la imaginación mediante cada contenido que se transmita en el aula.

En función de los datos obtenidos, cuando en el abordaje didáctico se estimula la función de seriación en el estudiantado, esta colabora medianamente en el progreso de las funciones de identidad, lateralidad, correspondencia y comparación. Sin embargo, ejercitar la seriación estimula directamente la clasificación. La seriación es una parte fundamental en el desarrollo de los niños, porque les ayuda a optimizar la parte cognitiva, lo que quiere decir que los estudiantes podrán establecer relaciones comparativas respecto a un sistema referencial. El uso de la creatividad en el salón de clase incentiva a mejorar las habilidades cognitivas del alumnado: relacionar, resolver, indagar e interpretar. De esta manera, el docente aportará para que ellos adquieran un mejor aprendizaje que les ayude a solucionar los problemas de la vida diaria con creatividad.

Según los datos obtenidos, la identificación favorece medianamente en los estudiantes el incremento de la clasificación. Así, además de ejercitar la identificación, también incentiva directamente el avance de la seriación y comparación. Desde este punto de vista, es de suma importancia analizar el problema para identificar el tipo de solución más adecuada. Un docente creativo es aquel que confía en sus estudiantes y les brinda espacios de participación, les deja expresarse, cree en sus capacidades y, lo más importante, no bloquea sus ideas.

Como se desprende de los datos extraídos en la prueba de correlación de Pearson, la función de clasificación en los estudiantes ayuda de alguna manera a potenciar la identificación, lateralidad, correspondencia y comparación. No obstante, ejercitar la clasificación impulsa claramente el progreso de las dimensiones de seriación. Hoy en día, la creatividad posee una gran importancia como eje transversal en las diferentes actividades del ser humano, principalmente dentro de la educación.

De igual manera, se ha puesto de manifiesto que en la función de lateralidad en los educandos colaboran medianamente para la seriación, clasificación y correspondencia, si bien ejercitar la lateralidad motiva directamente la comparación. La lateralidad es significativa para el proceso de aprendizaje de las matemáticas, por lo que requiere de un procesamiento de información para que el estudiante mejore sus habilidades numéricas. La didáctica en la educación revela formas, métodos de enseñanza y aprendizaje, estimulando el proceso educativo en todas las etapas de formación.

Teniendo en cuenta el análisis de la tabla de funciones para el alumnado se puede ver que la correspondencia colabora medianamente para mejorar las funciones de seriación, clasificación y lateralidad. En cambio, ejercita la correspondencia, puesto que estimula directamente la comparación. La didáctica es importante en la educación porque ayuda al docente a seleccionar y utilizar los materiales que facilitan las destrezas y los indicadores de evaluación, al tiempo que favorece la reflexión sobre las diferentes estrategias de aprendizaje.

En consecuencia, se pueden detallar los datos obtenidos en la función de comparación en los educandos, dado que coadyuva relativamente a las funciones de seriación, identificación clasificación y lateralidad. Sin embargo, ejercitar la comparación incita directamente a la correspondencia. El uso de las estrategias didácticas es relevante en el marco de la enseñanza y aprendizaje porque a través de ella se pueden enseñar de diferentes formas los contenidos matemáticos y lograr un conocimiento constructivo.

A partir de los hallazgos analizados se constata la conveniencia de los procesos didácticos creativos en la sección de aprendizaje de las matemáticas, para familiarizarse con los problemas y ejecutar estrategias con más alcance para los estudiantes en la comprensión de conceptos y análisis de resultados.

Carrión, E. (2019). El uso del juego y la metodología cooperativa en la Educación Superior: una alternativa para la enseñanza creativa. Universidad Camilo José Cela, 23, 70-97. doi. Recuperado de: http://dx.doi.org/10.6035/Artseduca.2019.23.4

Celi Rojas, S. Z., Quilca Terán, M. S., Sánchez, V. C., & Paladines Benítez, M. d. (julio-septiembre de 2021). Estrategias didácticas para el desarrollo del pensamiento lógico. Horizontes. Revista de Investigación en Ciencias de la Educación, 5(19), 834. Recuperado de: http://www.scielo.org.bo/pdf/hrce/v5n19/2616-7964-hrce-5-19-826.pdf

Delgado, P. (2019). Profundizando en el conocimiento: la reflexión como herramienta de aprendizaje. La reflexión ayuda al alumno a organizarse, comunicar sus pensamientos y comprender si realmente entienden un tema. Instituto para el Futuro de la Educación, Monterrey. Números (en línea). Recuperado de: https://repositorio.uta.edu.ec/jspui/handle/123456789/32854

Guaypatin Pico OA, Fauta Ramos SL, Gálvez Cisneros XA, Montaluis D. La influencia de la matemática en el desarrollo del pensamiento. bol.redipe [Internet]. 11 de julio de 2021 [citado 21 de noviembre de 2021];10(7):106-12. Recuperado de: https://revista.redipe.org/index.php/1/article/view/1352

Ordoñez Pardo, J. C., Coraisaca Quituizaca, E. C., & Espinoza Freire, E. E. (2020). "¿Se emplean recursos didácticos en la enseñanza de matemáticas en la educación básica elemental? Un estudio de caso". Revista Metropolitana de Ciencias Aplicadas, 3(3), 48-55. Recuperado de: https://remca.umet.edu.ec/index.php/REMCA/article/view/309

¹De acuerdo con el informe PISA-D Ecuador" el nivel de desempeño básico implica que los estudiantes saben interpretar y reconocer situaciones en contextos que solo requieren una inferencia directa. Los estudiantes de este nivel pueden extraer información de una única fuente y usar un único modo de representación. Los estudiantes pueden utilizar algoritmos, fórmulas, procedimientos o convenciones de nivel básico para resolver problemas que contengan números enteros. Son capaces de hacer interpretaciones literales de los resultados" (INEVAL-OCDE, 2018, p. 37).

Los autores participaron en la redacción del trabajo y análisis de los documentos.