Mendive. Journal on Education,april-june 2021; 19(2): 446-457

Translated from the original in Spanish

Difficulties in arguing the use of semiotic records in quadratic variation problems

Dificultades para argumentar el uso de registros semióticos en problemas de variación cuadrática

Dificuldades em sustentar a utilização de registos semióticos em problemas de variação quadrática

Wilmer Ríos-Cuesta¹ http://orcid.org/0000-0001-8129-2137

¹The Valle University. Colombia. wilmer.rios@correounivalle.edu.co

Received: January 30^th, 2021.
Approved: March 23^rd, 2021.

ABSTRACT

We present a qualitative case study with an experimental approach in which we sought to understand the lack of participation in class of a group of 14 9 ^th grade students in a public institution in the department of Chocó. We inquired about the operational issues they develop when solving a quadratic variation problem by presenting several semiotic registers of the task and focusing on the arguments they offer to justify their reasoning. We found a marked preference for the tabular register, although it is not the optimal one to solve the task, and a difficulty to offer arguments based on evidence that give more strength to their reasoning. Class participation should be promoted through open tasks, starting to develop argumentative processes in lower grades and minimizing teaching focused on memorization and application of algorithms to develop mathematical thinking.

Keyword: registries; semiotic representations; quadratic variation; argumentation; mediation.

RESUMEN

Se presenta un estudio de caso cualitativo con un enfoque experimental, en el que se buscó comprender la falta de participación en clase de un grupo de 14 estudiantes de 9° grado en una institución pública en el departamento del Chocó. Indagamos sobre las cuestiones operativas que desarrollan al momento de resolver un problema de variación cuadrática mediante la presentación de varios registros semióticos de la tarea y situando la mirada en los argumentos que ofrecen para justificar su razonamiento. Encontramos una marcada preferencia hacia el registro tabular, aunque no es el óptimo para resolver la tarea, y una dificultad para ofrecer argumentos basados en evidencias que le den mayor fuerza a su razonamiento. Se debe promover la participación en clase por medio de tareas abiertas, comenzar a desarrollar procesos argumentativos en grados inferiores y minimizar la enseñanza centrada en la memorización y aplicación de algoritmos para poder desarrollar pensamiento matemático.

Palabras clave: registros; representaciones semióticas; variación cuadrática; argumentación; mediación.

RESUMO

Apresentamos um estudo de caso qualitativo com um focus experimental na qual procurámos compreender a falta de participação na aula de um grupo de 14 alunos do 9º ano numa instituição pública do departamento de Chocó. Questionamos sobre as questões operacionais que desenvolvem quando solucionam um problema de variação quadrática, através da apresentação de vários registos semióticos da tarefa e concentrando-nos nos fundamentos que oferecem para justificar o seu raciocínio. Encontrámos uma preferência marcada pelo registo tabular, embora não seja o ideal para resolver a tarefa, e uma maior dificuldade em oferecer argumentos baseados em provas que dão maior força ao seu raciocínio. A participação nas aulas deve ser incentivada por meio de tarefas abertas, começando a desenvolver processos argumentativos nas notas mais baixas e minimizando o ensino baseado na memorização e aplicação de algoritmos, a fim de desenvolver o pensamento matemático.

Palavras-chave: registos; representações semióticas; variação quadrática; argumentação; mediação.

INTRODUCTION

Mathematics education from the study of the quadratic function is proposed, once students have some dominion of solving quadratic equations. In this process, students use techniques such as factoring through common factors, the sum product pattern, grouping, perfect square trinomials, difference of squares, completion of squares or the identification of the coefficients a, b and c to use them in the quadratic formula

Some of the problems that are proposed to the students and that deal with the study of the quadratic function require the calculation of the focus, vertex, cut-off points, maximums and minimums. However, the phenomena of quadratic variation at the school level have been left for the study of physics in problems related to projectile launching, where it is requested to calculate the maximum height, maximum range and flight time.

The approach quadratic variable that situations require that students be able to identify the variables, raise the equations and use a resolution method according to heuristics that have and have built along their learning process. This type of problems has given an Algebraic treatment that darkens the search for geometric solutions and it has reduced the shape of the curve. In particular, we intend to give the student several solution alternatives, which allow him to consolidate his thinking moving through various semiotic registers that mediate his cognitive activity such as graphic, tabular, analytical and verbal representation (Duval, 1993).

The justification for this study lies in providing theoretic elements to understand the lack of participation in mathematical activity performed in the classroom for a group of high school students in a public school in the department of Choco in Colombia.

We have noticed that in the classes there is an excessive use of algorithms, which are presented to the students as a finished work, there is an excessive memorization of contents and it is noted that the students evade the cognitive conflict by adhering to the explanations they their peers give. (Castellaro and Peralta, 2020).

To achieve the purpose of this study, the gaze is directed towards the production of arguments through the use of different semiotic registers of the activity that is carried out.

Studies on argumentation in Mathematics class have allowed us to analyze the discursive activity in the classroom around the individual or collective construction of valid arguments. Krummheuer (2007) conceives argumentation as a social phenomenon, with an emphasis on student interaction, and indicates that, learning of mathematics depends on the processes of argumentation that develop inside the classroom. In this regard, Rumsey & Langrall (2016) argue that argumentation gives students the possibility of socializing their procedures, responses and points of view about the mathematical activity they develop.

Rios-Cuesta (2020) comments that the arguments  offers the opportunity for students to remove doubts about their productions having to verbalize their ideas to the teacher, as a representative of the knowledge, to institutionalize the valid procedures, to make meaningful learning. It helps to develop the cognitive part and social interaction.

Chico (2018) points out that to develop argumentation in class the student requires higher levels of mathematical argumentation, due to the fact that they have to convince their classmates; this has a higher cognitive demand, which helps consolidate your thinking.

In addition, mathematical argumentation, seen as social practice in the classroom, aims to try to convince others or him on a point of view. This entails that students develop skills such as analysis of the arguments of his colleagues to consolidate or reject his reasoning.

Cervantes-Barraza & Cabañas-Sánchez (2018) offer a study on geometric argumentation using the Toulmin model. His research methodology was based on the design research paradigm with a qualitative approach through a teaching experiment. It stands out, among its findings, which students use diagrammatic arguments which are associated with the display of the object of study. However, their answers lack mathematical support, which is proof that students are moving away from the formalism of mathematics. However, the authors suggest the use of tasks in which exploration is encouraged by arguments based on guarantees.

Fiallo & Gutiérrez (2017) say that an argument is constituted through a string of verbal statements that are based on mathematical elements that seek to explain an outcome.

On the other hand, studies on argumentation maintain that it is generated through the interaction between the teacher and the student (Chico, 2018). However, in this study we place ourselves on the concept of interactivity (Coll, et al. 1992) defined as:

   […] The articulation of the actions of the teacher and the students [...] around a task or a specific learning content, thus calls attention to the importance of analyzing the actions of the students in close connection with the teacher's actions; and reciprocally (p. 204).

The concept of interactivity is broader than that of interaction, since it goes beyond verbal exchanges, it is understood as "the forms of organization of joint activity" (Coll et al., 1992, p. 192).

With this in mind we proceeded to inquire on operational issues that develop when solving a quadratic variation by presenting various semiotic registers of the task and placing look at the arguments offered to justify their reasoning.

MATERIALS AND METHODS 

We report a qualitative case study with an empirical experimental approach ( Stake, 2010), which seeks to describe and interpret the way in which students solve a quadratic variation problem, emphasizing not only the solution, but also the semiotic records and the arguments used to validate its position.

Two categories of analysis of the information collected were established, which allowed the analysis and interpretation of the productions.

In the first, we analyze the type of semiotic representation that students use to solve the problem.

In the second, we checked whether arguments were produced to support the solution of the task and the chosen solution model.

The course was made up with 14 high school students between 14 and 17, a public school in the department of Choco, which enrolled in ninth grade of   Basic Secondary Education in Colombia. A questionnaire with semi-open questions was used, where the students could argue the choice of a certain semiotic register to solve the proposed task and explain the procedure followed.

Pseudonyms are used in the dialogues to protect the identity of minors and thus comply with the ethical issues of the study.

The experience that allowed the data collection consisted of solving a task that asked students to find two positive integers whose sum is 30 and whose product is the maximum possible.

Various records were presented to them to inquire about preferences when communicating their results; in this way, try to understand how they understand the problem and lead them to use other types of representations. The various registers used in the study are presented below.

The tabular record presented in table 1 consists of assigning an increasing and a decreasing value so that the property that the sum is equal to 30 is fulfilled and their products are calculated.

Table 1-Tabular problem record

The second record presented is the algebraic one, made up of the system of equations,in which the conditions of the problem are shown , but the maximum sought value does not appear. This requires another type of analysis for its resolution and a greater cognitive demand.

In third instance the record chart was presented. It complements the tabular record and shows in the ordinate axis, the maximum value required in the algebraic register .

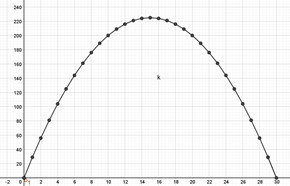
Fig. 1- Graphical record of the problem

The fourth register is the geometric one. It is constructed by transferring the information of the problem to rectangle sides and as shown in Figure 2. 

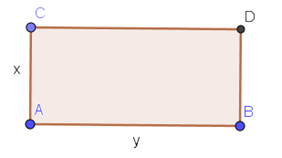
Fig. 2 - Geometric representation of the problem

This representation complies with the fact that:

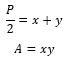
In this register it is assumed that the sum of the two numbers constitutes the semi perimeter of a rectangle with sides .

Another record chart that allows to achieve the solution of the problem consists of the point among the straight lines  resulting from and then find the inverse function of  this gives us a linear solution to the problem (figure 3).

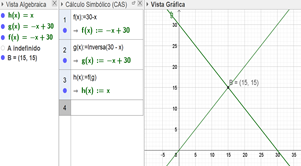
Fig. 3 - Linear solution of the problem

As an analysis tool, the model of Toulmin (2003) it is proposed to explain the structure of the arguments (figure 4). This model consists of the data D (data), the permissions infer Pi (warrant), the support S (backing), the indicator modal force F (modal qualifiers) of the argument, the potential refutations Rp (rebuttals) and the assertion E (claim).

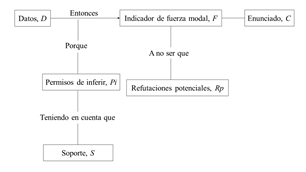
Fig. 4 - Toulmin model

Data D are facts or evidence to start the process of argumentation.

The permissions to infer Pi are a general rule or principle that serves as the foundation for moving from the data to the statement. It is manifested through a series of statements that seek to establish the relationship between the data and the statement.

The bracket S is the basis to infer permissions. This support permits inferring and provides valid reasons.

The modal strength indicator F shows the degree of certainty or the strength of the statement.

The potential rebuttals Rp are the exceptions to the assertion, particular cases or counter examples.

Statement C is the assertion that is reached as a result of the argumentation process.

When a person makes an argument, he takes the data into account and, according to his reading of it, makes a conclusion or statement. In this transition, the permission to infer is used, which builds a bridge between the data and the conclusion. In that sense, permission to infer a rule or principle that allows a logical connection, so that, when a rebuttal is made to the argument, what is questioned is the permission to infer; consequently, the student is immersed in a situation where they must make more explicit the permissions to infer. When the above situation occurs, the student can resort to the support to make explicit the permission to infer using justifications.

Although the model provides us with elements to analyze the structure of the arguments, Solar & Deulofeu (2016) indicate that rarely all the elements of the model appear in a class. In consequence, Molina -Jaime  et al., (2019) using one ternary structure model Toulmin (2003) based on the data, permissions to infer and conclusion (Figure 5).

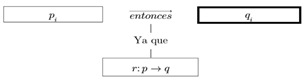
Fig. 5 - Ternary structure of the Toulmin model (Molina-Jaime  et al., 2019)

We consider, then, that there is an argument or if they are offer, at least, three elements of the model Toulmin described by Molina -Jaime et a l. (2019); However, the purpose of this study was not to characterize the students' arguments but to analyze their existence.

RESULTS

Initially they were asked to solve the problem of finding the two numbers that fulfilled the given conditions. The students worked individually for 20 minutes without the teacher's intervention. We highlight that only two students solved the task using a tabular representation.

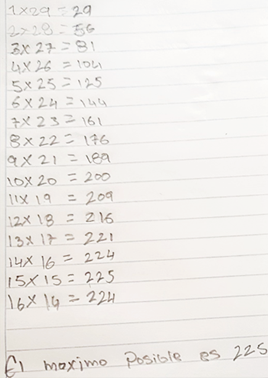
Fig. 6 - Individual response to task 1

After the presentation of the results, the students were asked to argue their productions; with this, an attempt was made to originate discussion and debate to try to superimpose one result on another.

In the speech that was originated in class, the students try to justify the choice of his conduct; It is highlighted the responses of three students that expressed the following:

Juan: We make a table that goes from 29 down and we are going to multiply that table with positive integers number, the number with the highest multiplication will be our maximum possible product. And in this case would be 15 since the sum gives 30 the product is 225.

Valentina: We add 15 + 15 and the result gives us 30 and when we multiply 15 × 15 the result it gives us is 225, when doing the multiplication with other numbers the result was less.

Nubia: I made a table with integers up to 30 which is the result we want to find and thus I realized that the two integers is [are] 15 [and 15] and whose sum gives us 30 as the result.

As the interest was to generate argumentation, they were asked to expand their choice a little more. We noticed a difficulty in generating arguments, as shown in the following student contribution:

Camilo: I used the form to solve the equation, which   was 15 +15= 30 y 15 x 15 = 225; and 225 is the maximum product.

Sebastian: Because the sum of these numbers really sums 30 and if they are multiplied, they give their maximum.

Marlon: We make a table that goes from 29 down and we are going to multiply that table with positive integers, the number with the highest multiplication will be our maximum possible product. And in this case would be 15 since the sum gives 30, the product gives 225.

Carla: first a table is made with all the whole numbers whose sum equals 30 and the product is the largest, then all the products are compared to find out which is the highest.

The students rely on algorithmic processes to show their results, it is not observed that the discursive activity points to confrontation, to convince or validate their productions, but rather they pretend to know a result. This highlights the absence of the argument as a rhetorical process to help persuade the audience, making it clear that we seek no logical formalism of argument.

Subsequently, five semiotics performances defined in this study to choose which they consider to present the best results were presented to the students. Option 1 corresponds to the tabular register, option 2 to the algebraic one, option 3 is the graphical one, option 4 is the geometric one, and option 5 is the graphical linear solution register.

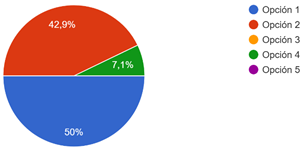
Fig. 7 - Preference for the different semiotic registers of the response

The trend towards registers one and two is observed, which are clearer for the presentation of the results; although record type one involves doing more accounts to complete the table.

Next, we present the justifications offered by the students for their choice:

Valentina: The option I chose (algebraic register) seems to me to be the clearest to handle, although it is a bit complex; however, option one is easier to handle.

Ruby: Because it is a table that clearly shows us the sum and its product.

David: A system of equations, I think it would give us a more accurate result. Besides that it is a somewhat simple and short way and, in the end, an aesthetic response.

Juan: Because this is the easiest but long way and it's the one I used.

Luisa: Because it is a table that clearly shows us the sum and its product.

The students' discourse aims to clarify their behavior, but not to give data, to be based on facts or evidence to make a solid argument.

DISCUSSION

As Crespo (2005) points out, an argument-based teaching helps you avoid memorizing algorithms and content that favor mechanical learning. However, in this study we can show that students find it difficult to argue their productions; there are difficulties in mathematical reasoning, which is observed when reviewing the semiotic register that they prefer to solve the problem.

The low cognitive demand identified in students has implications in the way they conceive mathematics and prevents them from entering into validation processes of their productions.

For them, mathematics has a utilitarian character, but not a functional one; it is seen as a tool to find a result that is rarely tested. As a consequence, the richness that the proposed task has, on an intellectual level, is not explored.

It must make a didactic turn and give the role students to validate their productions by arguments that must be debated and publicly defended, as an opportunity to learn mathematics. The teacher, as a representative of knowledge in class, has the duty to validate and approve accepted procedures in mathematics. However, the purpose of the students should not be the search for the validation of the teacher but rather the articulation of the ideas that the teacher offers with those of their peers and the conceptual richness of mathematical ideas.

Corroborate the thesis of Goizueta (2019), who points out that students have difficulty justifying what they do and say in the class of Mathematic, which makes it difficult to include complex mathematical tasks favoring planning of activities in which Students practice running algorithms prescribed by the teacher.

We agree with Goizueta (2019) that:

   Mathematics education should be concerned with the development of mathematical cultures in which the communication of epistemic issues is relevant and the willingness to do so prevails. If we expect teachers to mediate the development of classroom math culture, they should be able to engage in meaningful (Meta) math conversations with their students. When the relevant aspects of the students' (meta) mathematical activity are not communicated, the possibility of such mediation is compromised and the teacher can be relegated (involuntarily) to being a mere judge of technical performance. Therefore, learning mathematics is also learning what is worth communicating about mathematical activity (p. 10).

Although it seeks to generate cognitive imbalances in students to modify their cognitive structure, it is observed that they evade it and that they take the longest path, but with less cognitive demand.

With this study, we have tried to point adjacent difficulty to try to encourage the production of arguments class for high school students who have used memory as a way to learn math. These students are the product of traditional teaching in which teachers have a leading role in classes and students are spectators of the content presented.

We recognize that in the classrooms are spaces where the teacher must provide certain information, especially when detected voids or gaps on the subject to be treated; however, this may not be a constant in the math class, it should be promoted from lower levels, one transition to a classroom environment where students argue their products so that they are accustomed to this type of environment.

The time constraints to develop curricula established in the educational institutions of the country are one of the causes that explain the difficulty to change some practices in the classroom, it is important to develop gradually cognitive processes of higher order students to promote levels of thought lead them to question knowledge and reflect critically in front of society.

We note that there is a conflict in students when facing a task whose solution is not immediate, this is a consequence of the type of teaching to which they are accustomed where tasks are proposed that are solved by applying an algorithm already established in class.

On the other hand, it should promote cognitive tasks that have a sustained cognitive demand and by argumentation it allow the discussion of the results and allow the productions.

BIBLIOGRAPHIC REFERENCES

Castellaro, M., & Peralta, N. S. (2020). Pensar el conocimiento escolar desde el socioconstructivismo: Interacción, construcción y contexto, Perfiles Educativos, 52(168), 140-156. https://doi.org/10.22201/iisue.24486167e.2020.168.59439

Cervantes-Barraza, J., & Cabañas-Sánchez, G. (2018). Argumentos formales y visuales en clase de geometría a nivel primaria. Educación Matemática, 30(1), 163183. https://doi.org/10.24844/EM3001.06

Chico, J. (2018). Impacto de la interacción en grupo en la producción de la lengua del álgebra en clase de matemáticas. Avances de Investigación en Educación Matemática, 14, 31-47. https://doi.org/10.35763/aiem.v0i14.243

Coll, C., Colomina, R., Onrubia, J., & Rochera, M. J. (1992). Actividad conjunta y habla: una aproximación al estudio de los mecanismos de influencia educativa. Infancia y Aprendizaje, 15(5960), 189-232. https://doi.org/10.1080/02103702.1992.10822356

Crespo, C. (2005). La importancia de la argumentación matemática en el aula. Premisa, 24, 23-29. http://www.soarem.com.ar/Documentos/24%20Crespo.pdf

Duval, R. (1993). Registros de representación semiótica y funcionamiento cognitivo del pensamiento. En F. Hitt, (Ed), Investigaciones en Matemática Educativa II (pp. 173-201). Grupo Editorial Iberoamericana.

Fiallo, J., & Gutiérrez, A. (2017). Analysis of the cognitive unity or rupture between conjecture and proof when learning to prove on a grade 10 trigonometry course. Educational Studies in Mathematics, 96(2), 145-167. https://doi.org/10.1007/s10649-017-9755-6

Goizueta, M. (2019). Epistemic issues in classroom mathematical activity: There is more to students' conversations than meets the teacher's ear. The Journal of Mathematical Behavior, 55, 1-11. https://doi.org/10.1016/j.jmathb.2019.01.007

Krummheuer, G. (2007). Argumentation and participation in the primary mathematics classroom. Two episodes and related theoretical abductions. Journal of Mathematical Behavior, 26, 60-82. https://doi.org/10.1016/j.jmathb.2007.02.001

Molina-Jaime, Ó. J., Font, V., & Pino-Fan, L. (2019). Estructura y dinámica de argumentos analógicos, abductivos y deductivos: un curso de geometría del espacio como contexto de reflexión. Enseñanza de Las Ciencias: revista de investigación y experiencias didácticas, 37(1), 93116. https://doi.org/10.5565/rev/ensciencias.2484

Ríos-Cuesta, W. (2020). Competencias de argumentación y modelización en estudiantes de secundaria: la necesidad de un cambio de paradigma en la Educación Matemática del Chocó, Colombia. Pesquisa E Ensino, 1, 1-21. https://doi.org/10.37853/pqe.e202020

Rumsey, C., & Langrall, C. W. (2016). Promoting mathematical argumentation. Teaching Children Mathematics, 22(7), 412419. https://www.nctm.org/Publications/Teaching-Children-Mathematics/2016/Vol22/Issue7/Promoting-Mathematical-Argumentation/

Solar, H., & Deulofeu, J. (2016). Condiciones para promover el desarrollo de la competencia de argumentación en el aula de matemáticas. Bolema: Boletim de Educação Matemática, 30(56), 1092-1112. https://doi.org/10.1590/1980-4415v30n56a13

Stake, R. (2010). Qualitative research: studying how things work. The Guilford Press. https://www.amazon.com/-/es/Robert-Stake/dp/1606235451

Toulmin, S. (2003). The uses of argument (updated ed.). New York: Cambridge University Press. Original work published 1958. https://doi.org/10.1017/CBO9780511840005

Conflict of interest:

Author declares not to have any conflicts of interest.

Authors´ Contribution:

The author assumed individually the elaboration of this article.

This work is under a licencia de Creative Commons Reconocimiento-NoComercial 4.0 Internacional
Copyright (c) Wilmer Ríos-Cuesta