Las actitudes con relación a las matemáticas y el desempeño algebraico en la asignatura Matemática

Las actitudes con relación a las matemáticas y el desempeño algebraico en la asignatura Matemática

Attitudes in relation to mathematics and algebraic performance in the subject Mathematics

Atitudes em relação à matemática e ao desempenho algébrico no domínio da Matemática

Este artículo resume los resultados de una pesquisa cuyo propósito fue analizar el nivel de relación que se puede establecer entre las actitudes con relación a la Matemática, el desempeño en esta asignatura y en los contenidos del Álgebra, como uno de los temas esenciales a aprender por los estudiantes. Se utilizó un diseño cuantitativo. El trabajo de campo se realizó con 326 estudiantes, de dos escuelas de la Enseñanza Secundaria General en Angola. Se utilizó un cuestionario para la caracterización de las actitudes con relación a la Matemática, aplicando una escala de tipo Likert con 20 proposiciones (10 positivas y 10 negativas). También se hizo un análisis documental de los registros de evaluación en la asignatura de Matemática, de profesores y en la Secretaría de las escuelas, para determinar el desempeño de los sujetos investigados. Para el análisis de la información se utilizó la media, desviación estándar, varianza y el análisis de regresión para modelar las relaciones mediante ecuaciones. Los resultados señalan que existe evidencia de relación entre: el desempeño matemático y la actitud hacia la asignatura Matemática, entre el desempeño en Álgebra y la actitud con relación a la Matemática y entre el desempeño matemático y el desempeño en Álgebra.

This article summarizes the results of a research whose purpose was to analyze the level of relationship that can be established between attitudes in relation to Mathematics, performance in this subject and the contents of Algebra, as one of the essential topics to learn by the students. A quantitative design was used. The field work was carried out with 326 students, from two schools of the General Secondary Education in Angola. A questionnaire was used to characterize attitudes in relation to Mathematics, applying a Likert- type scale with 20 propositions (10 positive and 10 negative). A documentary analysis was also made of the evaluation records in the subject of Mathematics, of teachers and in the Secretary of the schools, to determine the performance of the investigated subjects. For the analysis of the information, the mean, standard deviation, variance and regression analysis were used to model the relationships using equations. The results indicate that there is evidence of a relationship between: mathematical performance and attitude towards Mathematics, between performance in Algebra and attitude in relation to Mathematics and between mathematical performance and performance in Algebra.

Este artigo resume os resultados de uma pesquisa cujo objectivo era analisar o nível de relação que pode ser estabelecido entre as atitudes em relação à Matemática, o desempenho neste assunto e nos conteúdos da Álgebra, como um dos tópicos essenciais a ser aprendido pelos estudantes. Foi utilizado um desenho quantitativo. O trabalho de campo foi realizado com 326 alunos, de duas Escolas Secundárias Gerais em Angola. Foi utilizado um questionário para caracterizar atitudes relativamente à matemática, aplicando uma escala do tipo Likert- com 20 proposições (10 positivas e 10 negativas). Foi também feita uma análise documental dos registos de avaliação na disciplina de Matemática, dos professores e do Secretário das escolas, a fim de determinar o desempenho das disciplinas investigadas. Para a análise da informação, a média, o desvio padrão, a variância e a análise de regressão foram usados para modelar as relações usando equações. Os resultados indicam que há evidência de uma relação entre o desempenho matemático e a atitude em relação ao tema Matemática, entre o desempenho em Álgebra e a atitude em relação à Matemática, e entre o desempenho matemático e o desempenho em Álgebra.

El papel de la enseñanza de la Matemática es de suma importancia para los estudiantes, según el Plan Curricular de la Enseñanza Secundaria General de la República de Angola, pues ella desarrolla el pensamiento lógico y es esencial para construcción de conocimientos en otras áreas, allende servir como base para las futuras profesiones (Ministério da Educação, 2019).

Es importante que la matemática juegue, de manera equilibrada e inseparable, su papel en la formación de capacidades intelectuales, en la estructuración del pensamiento, en la agilidad del razonamiento deductivo del alumno, en su aplicación a problemas, situaciones de la vida cotidiana y actividades en el mundo laboral y social en el apoyo a la construcción de conocimientos en otras áreas curriculares. (Ministério da Educação, 2019, p. 27).

La Ley de Bases del Sistema de Educación y Enseñanza de Angola (Assembleia Nacional, 2016) determina, en su artículo 30.º, que el Segundo Ciclo de la Enseñanza Secundaria es organizada en áreas de conocimiento de acuerdo con la naturaleza de los cursos a que da acceso y que comprende las 10ª, 11ª y 12ª serie. Ese cuadro contempla que es importante ofrecer a los alumnos de este ciclo oportunidades para interpretar problemas, comprender enunciados, utilizar informaciones dadas, establecer relaciones, interpretar resultados a la luz del problema orientado y enfrentar, con eso, situaciones nuevas y variadas.

Desde esta perspectiva, para analizar el proceso de enseñanza y el aprendizaje de Matemáticas en el Segundo Ciclo de la Enseñanza Secundaria, no se pueden desconsiderar los actores incluidos en el proceso: el estudiante, el profesor y los componentes didácticos, y es en ese sentido que Meléndez, Caraballo, Páez (2017, p. 11) establecen que es primordial partir de los "conceptos derivados de sus vivencias, sus interacciones sociales y su experiencia personal, como expresión de conocimientos amplios y diversificados, que pueden enriquecer el abordaje escolar, formulando cuestionamientos, afrontando posibilidades, proponiendo alternativas a ser consideradas".

A pesar de indicar la resolución de problemas como una alternativa metodológica para enseñar Matemática, el Plan Curricular de la Enseñanza Secundaria General en Angola (Ministério da Educação, 2019) identifica una distancia entre las propuestas oficiales y la Matemática realmente enseñada en esa modalidad escolar y revela que es necesario avanzar en términos metodológicos, pues, en un estudio preliminar a la elaboración de la propuesta, se constató que la gran mayoría de los profesores aún desconoce el abordaje basado en la resolución de problemas como eje orientador del aprendizaje en matemática (Ministério da Educação, 2019) y que a pesar de que el 90 % de los profesores consultados enseñen las operaciones básicas, apenas 14 % enseñan a resolver problemas con esas operaciones.

Además de estas dificultades, para la construcción de la Propuesta Curricular para el Segundo Ciclo de la Enseñanza Secundaria, fueron hechos estudios preliminares donde la Matemática fue apuntada, por estudiantes y profesores, como la disciplina más difícil de ser aprendida, atribuyéndole mucho de la responsabilidad por el fracaso escolar de los adolescentes y jóvenes (Ministério da Educação, 2019). En esta perspectiva, se vuelve uno de los "filtros sociales" que selecciona los que avanzan y los que son retenidos en la educación básica, así:

Quienes abandonan la escuela lo hacen por diversos factores sociales y económicos, pero también porque se sienten excluidos de la dinámica de enseñanza y aprendizaje. En este proceso de exclusión, el fracaso en el aprendizaje matemático ha jugado un papel importante y determina la frecuente actitud de desapego, miedo y rechazo en relación a esta disciplina, que a los estudiantes les parece inaccesible y sin sentido. (Ministério da Educação, 2019, p. 5).

Promover actitudes positivas en los alumnos, según Araya y Moreira (2016), debe ser objeto de acción de los educadores matemáticos. De esta forma, pueden aportar para que los estudiantes amplíen la autonomía, establezcan correctamente una autorreflexión y experimenten placer en la solución de problemas. La escuela es un espacio para suscitar actitudes positivas con relación a las materias escolares y, en consecuencia, a la Matemática.

En el proceso de comprensión de la actitud, conforme la concepción indicada por Abraham et al. (2010), la relación se establece entre los componentes cognitivo, afectivo y conductual. El aspecto afectivo de la actitud con respecto a la Matemática envuelve los sentimientos, emociones y el afecto que el individuo experimenta ante un objeto o situación, o sea, es el hecho de gustar o no de Matemáticas. El aspecto cognoscitivo envuelve el conocimiento, mientras el conductual se refiere a la expresión del conocimiento y del afecto. En esta concepción, las actitudes no son innatas, pueden ser progresadas y transformadas.

Por comprender que el aprendizaje dinamiza múltiples aspectos y que el desempeño no puede disociarse del desarrollo de habilidades específicas y de la formación de actitudes positivas con relación a la Matemática, es que se desarrolla esta pesquisa. Fueron objetivos centrales:

Las distintas experiencias que un estudiante ha tenido respecto a las Matemáticas y su proceso de aprendizaje determinan, en parte, la forma en cómo estos se desenvuelven en la asignatura. Entender y plantear estrategias para atender la problemática que enfrentan los sujetos en el aprendizaje de la asignatura Matemática implica no solo el planteamiento de tareas adecuadas sino tener en cuenta aspectos personales como sus actitudes. Razón por la cual el objetivo de este trabajo persigue analizar el nivel de relación que se puede establecer entre las actitudes con relación a la Matemática, el desempeño en esta asignatura y el desempeño en los contenidos del Álgebra como uno de los temas esenciales a aprender por los estudiantes.

Los sujetos de la presente investigación fueron todos los estudiantes de la 12ª serie de las escuelas Complejo Escolar "Delegado Eusebio Nelson" y el Complejo Escolar "Samacaca" en el municipio Tchitato, situado en el extremo nordeste de la provincia de Lunda-Norte en Angola, y ocupa una extensión territorial de 8.279 Km² que corresponde al 24,5 % del territorio de la Provincia (Administración Municipal de Tchitato, 2018). En cada una de las instituciones se trabajó con todas las secciones de la 12ª serie de estos colegios, por lo que no se utilizó ninguna muestra. En total fueron 326 alumnos, de los cuales 149 (45.7 %) son del género femenino y 177 (54.3 %) del género masculino. La edad de los discentes osciló entre 18 y 22 años. El 53.6 % de la población estudiada tenían 19 años.

La pesquisa fue realizada con estudiantes que estuvieran en el último año de la Enseñanza Secundaria General, de las instituciones educativas anteriormente presentadas y se verificó que todos los sujetos poseyesen registros de desempeños de los contenidos abordados en la asignatura Matemática en los cuadernos, de asistencia y evaluación, de los profesores y en la secretaría de las escuelas, en particular sobre el tema cinco que contiene los contenidos algebraicos. El registro de desempeño es esencial, pues, después de la aplicación del cuestionario de caracterización de los sujetos y de la escala de actitud con relación a la Matemática, se identificó el desempeño en la asignatura en la secretaría de la escuela.

El cuestionario para caracterización de los sujetos de la pesquisa fue elaborado a partir de Carvalho (1995), con la finalidad de lograr información por parte de los entrevistados. La escala de actitudes con relación a la Matemática fue adaptada y validada por Brito (1998) y es del tipo Likert con 20 proposiciones (10 positivas y 10 negativas), que intentan expresar el sentimiento que cada individuo posee con relación a la Matemática.

Cada proposición positiva recibió una puntuación, distribuida de la siguiente forma: concuerdo totalmente = 4 puntos, concuerdo = 3 puntos, desavengo = 2 puntos y desavengo totalmente = 1 punto; las negativas son puntuadas como: concuerdo totalmente = 1 punto, concuerdo = 2 puntos, desavengo = 3 puntos y desavengo totalmente = 4 puntos. Con eso, la puntuación de la escala de actitudes varía de un mínimo de 20 a un máximo de 80 puntos, indicando, respectivamente, actitudes más negativas y más positivas. En ese tipo de instrumento, ninguna proposición es considerada cierta o equivocada, pues apenas reflejan las expresiones de los sujetos en cuanto al sentimiento que experimentan frente a cada uno de los enunciados.

Por lo tanto, las hipótesis que se pretendieron comprobar para los alumnos participantes en el estudio, fueron:

Para clasificar las actitudes de los alumnos en positivas o negativas, se utilizó la media general como punto de corte; o sea, se consideró a los alumnos que presentaron puntuación por encima de la media como de actitudes positivas y aquellos que presentaron puntuación por debajo de la media, actitudes negativas. Como la media de la actitud de este grupo fue de 57,94 puntos con una desviación estándar de 11,65 puntos y valores mínimo de 23,00 y máximo de 80,00 puntos, podemos concluir que la actitud con relación a la Matemática de ese grupo de sujetos es positiva.

La tabla 1 presenta la distribución de las respuestas de los sujetos, bien como la media y la desviación estándar para cada uno de los aspectos de la escala, que muestra que los resultados medios de todas las proposiciones tienden más para resultados positivos que negativos. En ella podemos observar que la proposición media más baja que presentó fue la número 18: "Yo me pongo más feliz en la clase de Matemáticas de lo que en la clase de cualquiera otra materia". Siendo así, como la clase de Matemáticas no es considerada, por la mayoría, como aquella en que ellos se sienten más felices, es un indicativo para que los profesores de esta asignatura hagan orientaciones para tornarla más agradable. Por otro lado, las proposiciones que presentaron medias más altas y, por tanto, resultados más positivos fueron las de número 2: "No me gusta las matemáticas y me asusta tener que hacer esa materia", y las de número 3: "Hallo la Matemática muy interesante y me gustan las clases de Matemáticas". Eso significa que esos alumnos de la 12ª serie de ambas instituciones le gustan la disciplina y la consideran interesante.

Así, aunque las clases de Matemáticas no sean aquellas en que los alumnos se ponen más felices, ellos gustan de la asignatura. En cuanto a las clases, los sujetos pesquisados no se asustan en tener que cursarla y la consideran interesante.

Tabla 1- Distribución de las respuestas de los sujetos, de la media y de la desviación estándar y de la naturaleza de las proposiciones, para cada uno de los aspectos de la Escala de Actitudes con relación a la Matemática

Nº	Proposiciones	Naturaleza de la proposición*	Media e Desviación estándar	Concuerdo totalmente	Concuerdo	Desavengo	Desavengo totalmente
1	Yo me quedo siempre bajo una terrible tensión en la clase de Matemáticas	N	M = 2,89 DS = 0,96	30 9,2 %	76 23,3 %	115 35,3 %	105 32,2 %
2	No me gustan las matemáticas y me asusta tener que hacer esa materia	N	M = 3,25 DS = 0,83	11 3,4 %	46 14,1 %	119 36,5 %	150 46,0 %
3	Yo hallo la Matemática muy interesante y me gustan las clases de Matemáticas	P	M = 3,20 DS = 0,77	123 37,7 %	157 48,2 %	34 10,4 %	12 3,7 %
4	La Matemática es fascinante y divertida	P	M = 2,85 DS = 0,85	73 22,4 %	154 47,2 %	77 23,6 %	22 6,7 %
5	La Matemática me hace sentir seguro y es, al mismo tiempo, estimulante	P	M = 2,92 DS = 0,86	96 29,4 %	116 35,6 %	100 30,7 %	144,3%
6	No consigo pensar claramente cuando estudio Matemática	N	M = 2,66 DS = 0,93	35 10,7 %	111 34,0 %	111 34,0 %	69 21,2 %
7	Tengo sensación de inseguridad cuando me esfuerzo en Matemática	N	M = 2,72 DS = 0,92	38 11,7 %	80 24,5 %	142 43,6 %	66 20,2 %
8	La Matemática me deja inquieto, descontento, irritado e impaciente.	N	M = 3,02 DS = 0,89	19 5,8 %	65 20,0 %	130 40,0 %	112 34,4 %
9	El sentimiento que tengo con relación a la Matemática es bueno	P	M = 3,11 DS = 0,71	88 27,0 %	196 60,1 %	31 9,5 %	11 3,4 %
10	La Matemática me hace sentir cual si estuviese perdido en una selva de números y sin encontrar la salida	N	M = 2,95 DS = 0,90	19 5,8 %	81 25,0 %	123 37,7 %	103 31,6 %
11	La Matemática es algo que yo aprecio considerablemente	P	M = 3,00 DS = 0,79	27 8,3 %	38 11,7 %	165 51,0 %	96 29,4 %
12	Cuando yo oigo la palabra Matemática, tengo un sentimiento de antipatía	N	M = 3,00 DS = 0,86	27 8,3 %	38 11,7 %	165 50,6 %	96 29,4 %
13	Yo encaro la Matemática con un sentimiento de indecisión, que es resultado del miedo de no ser capaz en Matemática	N	M = 2,82 DS = 0,94	30 9,2 %	84 25,8 %	123 37,7 %	89 27,3 %
14	Me gustan realmente las Matemáticas	P	M = 2,89 DS = 0,93	88 27,0 %	150 46,0 %	54 16,6 %	3410,5 %
15	La Matemática es una de las materias que realmente me gusta estudiar	P	M = 2,84 DS = 1,00	100 30,6 %	111 34,0 %	77 24,0 %	3811,7 %
16	Pensar sobre el deber de resolver un problema matemático me deja nervioso	N	M = 2,79 DS = 0,89	27 8,2 %	88 27,0 %	138 42,3 %	7322,4 %
17	Nunca me gustó la Matemática y es la materia que me da más miedo.	N	M = 2,95 DS = 0,89	27 8,2 %	54 16,6 %	154 47,2 %	91 28,0 %
18	Yo me pongo más feliz en la clase de Matemáticas de lo que en la clase de cualquiera otra materia	P	M = 2,64 DS = 0,98	69 21,2 %	115 35,3 %	92 28,2 %	50 15,3 %
19	Yo me siento tranquilo en Matemática y aprendo de esa materia	P	M = 2,73 DS = 0,92	65 20,0 %	145 44,5 %	77 23,6 %	39 12,0 %
20	Tengo una reacción muy positiva con relación a la Matemática: me gusta y aprecio esa materia	P	M = 2,78 DS = 0,96	76 23,3 %	142 43,6 %	65 20,0 %	43 13,2 %

Como el análisis se realizó en dos escuelas diferentes, se supuso que la actividad pedagógica en ellas pudiese interferir en la actitud de los estudiantes hacia la asignatura Matemática y con esos datos se organizó la tabla 2.

Tabla 2- Estadística descriptiva de las actitudes de los sujetos investigados según la escuela de procedencia.

El análisis de la varianza aplicada a los datos de la tabla 2 no reveló diferencia significativa [F (2, 79) = 2,104; p < 0,05], lo que permite afirmar que el trabajo pedagógico realizado en las escuelas de procedencia no interfirió en la actitud de los estudiantes investigados hacia la Matemática. Esta es una constatación relevante, pues los estudiantes de ambas escuelas viven procesos formativos diversos, tanto con relación a la estructura organizativa de la escuela, los profesores diferentes y sus metodologías, entre otras variables influyentes, asimismo, no presentan variaciones significativas en la actitud con relación a la Matemática.

El desempeño en Álgebra tuvo como referencia los contenidos del tema cinco de los programas curriculares. Como se pretende que no bastaba con conocer el desempeño en el tema cinco sobre los contenidos algebraicos y su posible correlación con la actitud, se decidió utilizar parámetros para conocer el desempeño general, o sea, el desempeño matemático de los alumnos y, también, posibles correlaciones con la actitud.

Para lograr el desempeño en Matemática se utilizó la media de los registros de desempeños de la Secretaria de las escuelas y, con eso, la media de ese grupo de sujetos fue de 78,41, con una desviación estándar de 12,31, siendo la nota mínima de 51,86 y la máxima de 100,00 puntos. En Álgebra la media fue de 76,02, con una desviación estándar de 16,99, siendo la nota mínima de 50,00 y la máxima de 100,00 puntos.

La nota en los contenidos de Álgebra y la media aritmética en Matemática presentaron una correlación positiva y fuerte [r (85) = 0,784; p < 0,001]; utilizando el análisis de regresión para modelar esa relación logramos la ecuación

siendo X la media aritmética en Matemática y Y la puntuación lograda en Álgebra, con un coeficiente de determinación r² = 61,4 %. Eso significa que, para cada punto a más en la media aritmética en Matemática, el sujeto aumentaba en 1,08 puntos el valor de la nota en Álgebra (ver figura 1). Además, el coeficiente de determinación nos permite considerar que el 61,4 % de la variación de las puntuaciones de la nota en Álgebra podría ser explicada por la variación de las puntuaciones de la media aritmética en Matemática.

Los resultados señalan que existe evidencia de relación entre el desempeño en Matemática y el desempeño en Álgebra, que permite afirmar que, para esa muestra, cuanto mayor es el desempeño en Álgebra, mejor es el desempeño en Matemática y viceversa.

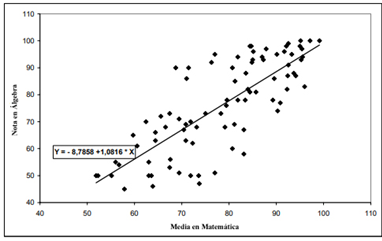
Fig. 1- Distribución de la nota en Álgebra con relación a la media en Matemática

Comparando la media aritmética en Matemática y la actitud encontramos una correlación positiva y comedida [r (85) = 0,460; p < 0,001] y a través del análisis de regresión modelamos esa relación como

, siendo X la media aritmética en Matemática y Y la puntuación relativa a la actitud, con un coeficiente de determinación r² = 21,2 %. Eso significa que, para cada punto a más en la media aritmética en Matemática, el sujeto aumentaba en 0,44 puntos el valor de la actitud (ver figura 2) y, además, el coeficiente de determinación nos permite considerar que el 21,2 % de la variación de las puntuaciones de la actitud puede ser explicada por la variación de la media aritmética en Matemática.

Los resultados señalan que existe evidencia de relación entre el desempeño matemático y la actitud hacia la asignatura Matemática, o sea, la actitud con relación a la Matemática influencia y es influenciada por el desempeño en Matemática.

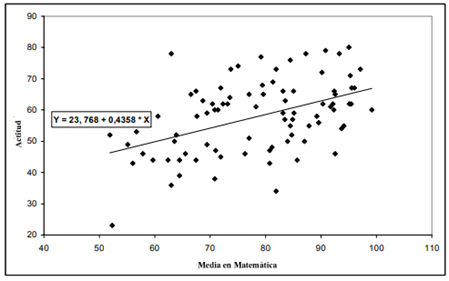
Fig. 2- Distribución de las puntuaciones de la actitud con relación a la media en Matemática

La nota en Álgebra y la actitud presentaron una correlación positiva y comedida [r (85) = 0,349; p < 0,01] y el análisis de regresión permitió modelar esa relación de acuerdo con la ecuación

, siendo X la nota en Álgebra y Y la puntuación relativa a la actitud, con un coeficiente de determinación r² = 12,2 %. Eso significa que, para cada punto a más en la nota en Álgebra, el sujeto aumentaba en 0,24 puntos el valor de la puntuación de la actitud (ver figura 3). Además, el coeficiente de determinación nos permite considerar que el 12,2 % de la variación de las puntuaciones de la actitud puede ser explicada por la variación de la nota en Álgebra.

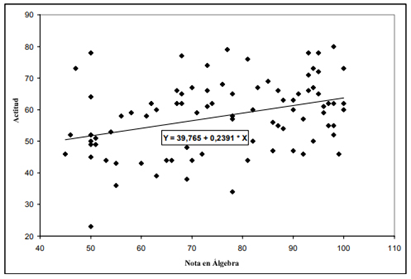
Fig. 3- Distribución de las puntuaciones de la actitud con relación a la nota en Álgebra

Los resultados señalan que existe evidencia de relación entre el Álgebra y la actitud con relación a la Matemática; o sea, la actitud con relación a la Matemática influye y es influenciada por el desempeño en Álgebra.

Las deducciones de la pesquisa llevan a inferir que los estudiantes del 2^o ciclo de la Enseñanza Secundaria que fueron investigados le gustan las Matemáticas, pues fue encontrada una actitud positiva con relación a ella; luego, para los sujetos de este estudio, los resultados contrarían la idea divulgada, en la informalidad, que los escolares no aprecian esta asignatura.

Propiciar experiencias emocionales propuestas es uno de los indicadores de cómo utilizar las variables afectivas en favor de la enseñanza. Por tanto, si el profesor conoce los factores que interfieren en el aprendizaje y en la enseñanza de Matemáticas, planeará adecuadamente las actividades e intervendrá en el proceso, posibilitando el desarrollo de actitudes positivas. Estas intervenciones son deseables, pues entendemos que la actitud se transforma y puede ser enseñada.

Sobre el desempeño del estudiante, el análisis de los datos indicó que existe una fuerte relación entre desempeño en Matemática y el desempeño en Álgebra, que permite afirmar que, para este grupo, cuanto mayor es el desempeño en Álgebra mejor es el desempeño en Matemática.

En las relaciones del desempeño con la actitud se constató que, para los sujetos investigados, los resultados encontrados indican que la actitud con relación a la Matemática está directamente relacionada tanto al desempeño en Matemática como al desempeño en Álgebra, en el 2⁰ Ciclo de la Enseñanza Secundaria General. Esto significa que, cuanto mejor es el desempeño en Álgebra, o en Matemática, mejor es la actitud con relación a la Matemática. Estos resultados son confirmados por Petriz, Barona, López & Quiroz (2010), cuyos estudios constataron que los estudiantes que tienen mejor desempeño presentan las mejores actitudes.

Para esta muestra, se evidenció que las actitudes con relación a la Matemática influencian y son influenciadas tanto por el desempeño en Matemática, como por el desempeño en Álgebra, pero cuando afrontamos los datos de la relación de la actitud con el desempeño en Álgebra y en Matemática, apareció una correlación más fuerte entre la actitud y el desempeño en Matemática de lo que entre la actitud y el desempeño en Álgebra.

Las acciones del profesor de Matemáticas, como de los profesores de las demás áreas, no pueden generar la enseñanza de actitudes negativas con relación a la Matemática, pues el discurso de muchos educadores refuerza la idea de que la mayoría de los estudiantes son incapaces de aprender Matemática.

Si las actitudes negativas o los estados de ansiedad hacia la disciplina han bloqueado la capacidad de razonamiento, es clave la toma de conciencia y la autorregulación por parte del alumno; en este sentido, la metodología del profesor es uno de los medios para lograr un cambio. Atender la parte emocional de los estudiantes debe ser una acción diaria para los docentes, ya que los estudiantes, como seres complejos, tienen emociones que están presentes en todo momento y en toda actividad, y que, por lo tanto, forman parte de su aprendizaje; sin embargo, en la clase de Matemática sus manifestaciones pocas veces son atendidas de manera adecuada.

Para el profesor resulta apreciable comprender la actitud de los alumnos hacia la asignatura, para ayudar a explicar algunos de sus comportamientos, así como para conocer sus capacidades, necesidades y adaptar las intervenciones educativas según las exigencias del contexto.

Conforme Meléndez y Baptista (2019), en los Programas Curriculares Nacionales se identifican dos grandes problemas en la enseñanza de Matemática en Angola: la necesidad de transformación de una realidad donde aparece la asignatura Matemática como un "fuerte filtro social", seleccionando aquellos que concluirán la enseñanza general, o no, y la necesidad de que la enseñanza de la Matemática crezca en calidad y aporte para la formación del ciudadano.

El significado de la Matemática en la formación de adolescentes y jóvenes es indicado por el Plan Curricular de la Enseñanza Secundaria General. En la propuesta curricular se afirma que:

A disciplina de Matemática desempenha um lugar de importante valor a todos os jovens neste ciclo de ensino, o que lhe permite desenvolver a capacidade de analisar e resolver situações problemáticas. A sua natureza permite ao jovem um conjunto de atitudes, capacidades e conhecimentos através do raciocino lógico e da comunicação (Ministério da Educação, 2019, p. 32)

E indica, también, que la escolarización representa una búsqueda de construcción de estrategias para la transformación del cuadro de exclusión vivido en Angola; luego, se proyecta que el currículo de Matemáticas debe contribuir a la formación de este individuo de tal forma que él pueda participar más activamente en el mundo del trabajo, de las relaciones sociales, de la política y de la cultura y ser protagonista de cambios en el ambiente en el que vive (Ministério da Educação, 2019).

En el Plan Curricular de la Enseñanza Secundaria General el bloque Pensamiento Algebraico orienta para que sean exploradas situaciones de aprendizaje que desarrollen las capacidades de reconocimiento de las representaciones algebraicas como generalizaciones aritméticas, traducción de situaciones-problema y favorecimiento de soluciones; de traducción de informaciones de tablas y gráficos para el lenguaje algebraico y de esta para el lenguaje gráfico, generalizando regularidades y posibilitando la identificación de los significados de las variables; construcción de estrategias de cálculo algebraico, a través de la utilización de conocimientos sobre operaciones aritméticas, produciendo e interpretando diferentes objetos algebraicos, como igualdades y desigualdades, identificando las ecuaciones, inecuaciones y sistemas; solución de problemas a través del uso de ecuaciones e inecuaciones del primer grado, comprendiendo los procedimientos envueltos; observación de regularidades y obtención de leyes que las expresan (Ministério da Educação, 2014).

Con relación a la enseñanza del Álgebra, Meléndez y Sánchez (2019) advierten que la dificultad de aprendizaje del cálculo riguroso, como de las operaciones algebraicas, es la hipótesis de que estos contenidos son introducidos de forma abstracta y desarrollada mecánicamente. Indica que:

El inicio del aprendizaje debe ser hecho desde el estudio de variación de cantidades en cuanto a un pequeño número de casos particulares, aumentando progresivamente los casos envueltos, para que el alumno pueda analizar regularidades que caracterizan esas variaciones y solo después intentar algún tipo de generalización (Meléndez y Sánchez, 2019, p. 5).

Al analizar las dificultades presentadas por los alumnos en el aprendizaje de Álgebra, Booth (1995) y Meléndez, Caraballo, Páez (2017) consideran que el Álgebra y la Aritmética, a pesar de sus diferencias, no son separadas, y que, en varios aspectos el álgebra se presenta como una aritmética generalizada. Para los autores, la fuente de dificultades en el álgebra es la aritmética, o sea, las relaciones y procedimientos aritméticos no aprehendidos afectan el desempeño en Álgebra, entonces las dificultades en álgebra "no son tanto de álgebra propiamente dicha, pero de problemas en aritmética que no fueron corregidos" (Booth, 1995, p. 33).

Booth (1995) determinó indicadores del por qué es difícil para los estudiantes aprender álgebra, desde la averiguación de errores cometidos con más frecuencia y distinguió que las causas de los errores podían estar en el origen de algunas ideas que los estudiantes tienen sobre: la actividad algebraica y la naturaleza de las respuestas; el uso de la anotación y de la convención de los objetos algebraicos; el significado de las variables; los tipos de relaciones y métodos usados en aritmética.

Al tratar de pasar de la aritmética para el álgebra, Meléndez, Caraballo, Páez (2017) dice que la principal novedad en el álgebra es el uso de las variables, y constató que los profesores percibían que la gran dificultad de los estudiantes, al pasar de los números de la aritmética para las variables del álgebra, era con relación al significado de las variables.

Además de las discusiones presentadas sobre algunas dificultades en el aprendizaje de álgebra, se considera pertinente la preocupación encontrada en Dorier (2002) al argumentar que los alumnos necesitan ser llevados a percibir que es ventajoso utilizar el álgebra para solucionar problemas, o sea, la utilización del método algebraico simplifica la solución de muchas situaciones-problema. En esa misma trayectoria, Dorier (2002) resalta que los estudiantes harán mejor uso de los recursos del álgebra para solucionar problemas, se percibe que los métodos informales que utilizan pueden limitar algunas situaciones y concluirán, por la experiencia, que para solucionar otros problemas más difíciles, necesitan procedimientos formales.

Otro aspecto destacado por Meléndez, Caraballo, Páez (2017) es que la escuela tiene el deber de propiciar actividades para los estudiantes, de tal forma que ellas auxilien en la construcción de un aprendizaje significativo del álgebra formal, para que los sujetos sean capaces de ligar los nuevos conocimientos a los conocimientos previos que ya poseen, conectando y dando sentido a los objetos algebraicos. Si el aprendizaje del álgebra es centrado simplemente en la manipulación de expresiones simbólicas, desde reglas que se refieren a entes abstractos, muy temprano los alumnos encontrarán dificultades en los cálculos algebraicos y pasarán a confundir las reglas de transformación algebraica, supuestamente aprendidas, aplicándolas cuando ellas no son válidas.

En este sentido, la motivación, la valoración o la disposición hacia las Matemáticas han sido uno de los factores intrínsecos asociados al rendimiento escolar, al igual que las actitudes y aptitudes del alumnado (Araya y Moreira, 2016). Relacionado con lo anterior, Demicheli (2009) indica que las actitudes son constructos teóricos fundamentales en el estudio, descripción, explicación y predicción de la conducta de los individuos, pues representan un indicio de sus experiencias pasadas y poseen influencia directa sobre su quehacer diario y proyección hacia el futuro.

El acceso a las actitudes relativas a la Matemática es un pequeño terreno de una gran tarea que es la de enseñar y propiciar modificaciones en las actitudes de los alumnos, buscando mejorar la autorreflexión y el desempeño de los mismos (Araya y Moreira, 2016).

Aún con relación al concepto de actitud, Demicheli (2009) observa que hay mucha confusión con relación al término actitud, siendo que muchos confunden actitudes con sus correspondientes, como comportamiento, me gusta, valores y creencias, para quien los significados atribuidos a la actitud no siempre son consensuados; generalmente la actitud aparece ligada a aspectos afectivos.

Algunas definiciones de actitudes, elaboradas por diferentes autores presentan puntos comunes, como: predisposición, aceptación o rechazo, favorable o desfavorable, positiva o negativa, aproximativa o evasiva (Demicheli, 2009).

Las actitudes pueden considerarse como representaciones psicológicas de la influencia que ejerce cada sociedad y cultura sobre las personas en tanto individuos. Por un lado, son inseparables de los contextos que la generan, mantienen y actualizan bajo ciertas condiciones, pero al mismo tiempo son una expresión que articula un conjunto más o menos amplio de experiencias individuales únicas. Estas representaciones psicológicas están presentes en todos los individuos, dirigidas a objetos, acontecimientos o personas, que asumen diferentes direcciones e intensidad de acuerdo con las experiencias del individuo (Demicheli, 2009, pp. 95-96).

Entonces, se puede decir que la actitud puede ser aprendida, y existen tres componentes que constituyen una actitud: el cognitivo, que incluye las ideas y percepciones sobre el objeto de la actitud; el afectivo, que corresponde a los sentimientos que el sujeto tiene y la intensidad de los mismos; y el conductual, dada por la respuesta que el sujeto tiene en reacción al objeto de la actividad (Abraham, Mena, Rodríguez, Golbach, Rodríguez & Galindo, 2010). En esta perspectiva, concebir y definir actitud significa envolver los dominios cognoscitivos (conocimiento), afectivos (sentimiento) y conductuales (predisposición para la acción).

La actitud se constituye en una condición psicológica necesaria para que el individuo realice una tarea con éxito. En particular, nos interesan las tareas matemáticas realizadas en la escuela y cómo pueden ser crecidas las actitudes de los alumnos cuando las ejecutan. En este sentido, Cárdenas (2008) considera que las actitudes se forman desde las experiencias, las actitudes con relación a la matemática influencian y son influenciadas por la enseñanza de esa disciplina, por la manera como ella es trabajada en la escuela, por la forma como los primeros conceptos básicos son adquiridos, por las habilidades que son exigidas del individuo y por el éxito o fracaso en la realización de tareas matemáticas.

Si las actitudes se forman desde las experiencias, el trabajo del profesor necesita ser envuelto para el desarrollo de actitudes favorables con relación a la escuela y a las disciplinas, aumentando la probabilidad de que sus alumnos desarrollen actitudes más positivas con relación a las mismas (Abraham et al., 2010).

Para Aiken y Aiken (1969) existen dos categorías de actitudes, ya consideradas como clásicas en este ámbito de las ciencias sociales: actitudes hacia la ciencia (cuando el objeto de la actitud es la propia ciencia) y actitudes científicas (si el objeto de la actitud son los procesos y actividades de la ciencia, esto es, la epistemología científica), asumidas después por distintos autores en el ámbito de la Matemática (Cárdenas 2008; GómezChacón, 2009; Petriz, Barona, López & Quiroz, 2010) como actitudes hacia la Matemática y actitudes matemáticas.

a) Actitudes hacia las Matemáticas, relacionadas con un conjunto de disposiciones que manifiesta el individuo para aceptar o no, familiarizarse o no, con determinados contenidos de la disciplina (Petriz, Barona, López & Quiroz, 2010). Pueden referirse a cualquiera de los siguientes aspectos:

b) Actitudes matemáticas, las cuales poseen carácter cognitivo y se refieren al "modo de utilizar capacidades como la flexibilidad de pensamiento, la apertura mental, el espíritu crítico, la objetividad, entre otras, consideradas como importantes para el aprendizaje de la disciplina" (Araya y Moreira-Mora, 2016, p. 30)

Considerando la importancia de las variables afectivas en favor de la enseñanza, el Plan Curricular de la Enseñanza Secundaria General en Angola hace algunas referencias sobre la actitud. En su parte introductoria, enfoca los aspectos emocionales y afectivos en el mismo grado de importancia que el cognitivo y afirman que ellos pueden interferir en el aprendizaje. En sus orientaciones, establece que la afectividad, el grado de aceptación o rechazo, la competitividad y el ritmo de producción establecidos en un grupo interfieren derechamente en la producción del trabajo (Ministério da Educação, 2019).

Los programas de la asignatura consideran los contenidos actitudinales como fundamentales en el rescate de la autoestima de los estudiantes de la Enseñanza Secundaria, pues las experiencias anteriores, de fracaso y de exclusión, les llevan, casi siempre, a construir una imagen negativa de la escuela y de sí mismos. Con eso, la imagen que tienen de la escuela, del aprendizaje y su autoimagen, necesitan ser reconstruidas, pues, para ellos, el valor de la escuela sobrepasa la adquisición de los conocimientos (Ministério da Educação, 2014).

Entre los muchos desafíos que un profesor de Matemáticas de la Enseñanza Secundaria enfrenta, está el de desarrollar un sentimiento de confianza, de actitud positiva, estableciendo metas de superación para sus sujetos que desconfían de las propias capacidades por las historias vividas de fracaso escolar.

También se conoce que la evaluación del desempeño en Matemática es realizada a través del uso de instrumentos como pruebas, trabajos individuales y trabajos en grupo, entre otros. Los valores atribuidos a esas actividades es que son comprendidas como el desempeño de los individuos en esta asignatura que puede ser considerado bueno, cuando las anotaciones son altas o malas cuando las anotaciones son bajas. Para Meléndez, Caraballo, Páez (2017), esta calidad de "malas" conferida al desempeño, genera ansiedad y puede llevar al alumno a desmejorar aún más su desempeño, haciendo con él que adquiera una baja autoestima. En este sentido, el desempeño afecta las actitudes de los alumnos.

Ampliando la relación entre desempeño y actitud, Aiken y Aiken (1969) establecen que la relación entre actitudes y desempeño es seguramente consecuencia de una influencia recíproca, en que actitudes afectan el desempeño y que el desempeño es afectado por las actitudes. Esto nos lleva a comprender que el sujeto, que no tiene éxito en Matemática, aquí entendido como buen desempeño, pasa a tener una actitud negativa con relación a la asignatura y esto hace que no se mueva en dirección a la apropiación de los contenidos matemáticos y, consecuentemente, no logra, de nuevo, un buen desempeño.

Se constituye, a juicio de los autores de este estudio, un círculo vicioso que puede ser quebrado desde que haya una intervención externa, en este caso del profesor, en el sentido de estar "liberando" la autoestima de este alumno y modificando su actitud con relación a la asignatura.

Como estas variables interfieren significativamente en el desempeño, se constituyen en indicadores para la actuación pedagógica que rubrique la construcción de actitudes positivas.

A juicio de los autores, el profesor que presente esta preocupación deberá dirigir sus acciones en el sentido de controlar la ansiedad y elevar la confianza. También necesita dejar claro cuál es el objetivo de la tarea propuesta, para que el alumno perciba que errando, se puede aproximar al objetivo propuesto que era desarrollar habilidades en la busca de la solución, de allí que las atribuciones de éxito y fracaso asumen otra perspectiva, o sea, no hay fracaso. Además, cuando el profesor presenta la dimensión práctica del contenido enseñado, influencia en la visión que el alumno posee de este, lo que puede motivarlo a aprender.

Abraham, G., Mena, A., Rodríguez, M., Golbach, M., Rodríguez, M., & Galindo, G. (2010). ¿La actitud hacia la matemática influye en el rendimiento académico? En P. Lestón (Ed.), Acta Latinoamericana de Matemática educativa, 23 (pp. 75-84), México. DF: Colegio Mexicano de Matemática Educativa A. C. y Comité Latinoamericano de Matemática Educativa A. C.

Aiken, R. L. y D. R. Aiken (1969), "Recent research on attitudes concerning science", Science Education, (53), pp. 295-305.

Assembleia Nacional. Angola. (2016). Decreto-Lei n.º 17/2016 de 4 de Abril- Lei de bases do Sistema de Educação e Ensino - Diário da República. Assembleia Nacional, Iª Série- N.º 65. Luanda: Imprensa Nacional.

Araya, R. y Moreira-Mora, T. E. (2016) Un modelo explicativo de las creencias y actitudes hacia las Matemáticas: Un análisis basado en modelos de ecuaciones estructurales. Avances de Investigación en Educación Matemática, (10), 27-51. Disponible en: https:www.researchgate.net/3117/pdf. Acceso 21/04/2020.

Brito, M. R. F. (1998). Adaptação e validação de uma escala de atitudes em relação à matemática. Zetetiké, 6(9), 109-162.

Booth, L. R. (1995). Dificuldades das crianças que se iniciam em álgebra. In: COXFORD, A. F.; SHULTE, A. P. (Org.). As ideias da Álgebra. Tradução de Hygino H. Domingues. São Paulo: Atual, p. 23-27.

Cárdenas, C. (2008). Identificación de tipologías de actitud hacia las matemáticas en estudiantes de séptimo y octavo grados de educación primaria. Perfiles Educativos, XXX(122), 94-108.

Carvalho, D. L. (1995) A interação entre o conhecimento matemático da prática e o escolar. 250 p. Tese (Doutorado). Faculdade de Educação, Universidade Estadual de Campinas, Campinas.

Demicheli, G. (2009). Calidad universitaria: actitudes y creencias de alumnos de 4^o de EM respecto de un subgrupo de universidades de la V región. Calidad en la educación, 31, 93-121.

Dorier, J.L (2002). Teaching Linear Algebra at University. En Li, Ta Tsien (ed.) et al. (2002). Proceedings of the international congress of mathematicians, ICM 2002, Pequín, China, 20-28 de agosto de 2002. Vol. III: Invited lectures. Beijing: Higher Education Press. 875-884.

Gómez-Chacón, I. M. (2009). Actitudes matemáticas: propuestas para la transición del bachillerato a la universidad. Educación matemática, 21(3), 05-32.

Meléndez, R., Caraballo, C., Páez, M. (2017). El currículum y la competencia profesional en la formación de profesores de matemáticas. Revista 2cenT. (01), Enero 2017. Editorial Unisan, Universidad Santander, Estados Unidos Mexicanos.

Meléndez, R. y Baptista, M. P. (2019). O currículum e a competência profissional na formação de professores de matemática. [ponencia]. I Conferência Internacional sobre Educação Matemática em Angola.

Meléndez, R. y Sánchez, R. (2019, 3-4 de julio). O caráter significativo, problemático, sistêmico e investigativo do processo de ensino-aprendizagem da álgebra linear [ponencia]. I Conferência Internacional sobre Educação Matemática em Angola.

Ministério da Educação. Brasil. (2019). Plano Curricular Ensino Secundário Geral. Editora Moderna, S.A. 1.ª Edição, Luanda, Angola.

Ministério da Educação. Brasil. (2014). Programas de Matemática - 10ª Classe, 11ª Classe, 12ª Classe. 2.º Ciclo do Ensino Secundário Geral. Editora Moderna, S.A. 2.ª Edição.

Petriz, M., Barona, C., López, R., & Quiroz, J. (2010). Niveles de desempeño y actitudes hacia las matemáticas en estudiantes de la licenciatura en administración en una universidad estatal mexicana. Revista Mexicana de Investigación Educativa, 15(47), 1223-1249. Consejo Mexicano de Investigación Educativa. Distrito Federal, México.

Los autores han participado en la redacción del trabajo y análisis de los documentos.

Escuela de formación	Cantidad de alumnos	Actitudes
Escuela de formación	Cantidad de alumnos	Media	Desviación Estándar	Mínimo	Máximo
Complejo Escolar “Delegado Eusebio Nelson”	203	59,92	10,295	35	78
Complejo Escolar “Samacaca”	123	56,72	13,373	37	79